隨機抽取replay memory有效的降低了資料跟資料的關聯，但帶來個問題樣本稀疏問題，像是大部分樣本對訓練是沒幫助的，以小恐龍來說很多時間是沒遇上仙人掌的。今天要講解prioritized replay就是要解決這問題，做採樣管理，讓重要的樣本有更多的機率被使用。

樣本稀疏問題

我們這邊先來做個舉例，讓replay memory的問題更清晰。如果我們現在玩一個很單純的單通道迷宮，遊戲結束目標為小智找到皮卡丘，動作限定只能走左跟走右，迷宮全貌如下。

如上所述條件，平常reward值為-0.1，而到達終點為1，state有7個。要完全到達終點的機率為2的7次方，代表要跑128次才會有一次正面樣本，而在隨機抽取情況下能取到正面樣本的機會非常低，這就是採樣稀疏問題，我們希望在這種情況下，能讓重要樣本有較大機會被選到。

transition

根據剛描述的採樣問題，我們可依據Q估計跟Q現實的差值(TD-error)，來量化出重要性，這個值我們稱transition，來做為選樣本的參考，但這種設計會有幾個問題：

1. target-net是定期更新，我們參考的transition值有可能是過去某時段的TD-error，所以這種方式作為評斷重要性，可能因為evaluate-net的參數改變，讓估計值跟實際值有落差。
2. 基於貪婪算法的性質，可能最新的transition更新完前幾次後就排到後面去了，導致容易選到的樣本都是離群值，TD-error大好更新的。
   基於上述，我們採取一種stochastic prioritization的方式，讓transition越大越容易被選到，transition值雖然小但仍有機會。

stochastic prioritization方法

stochastic prioritization實現有兩種方案，兩種都採取建築在以下機率公式上，因為篇幅有限，我們僅介紹第一種的實作方式：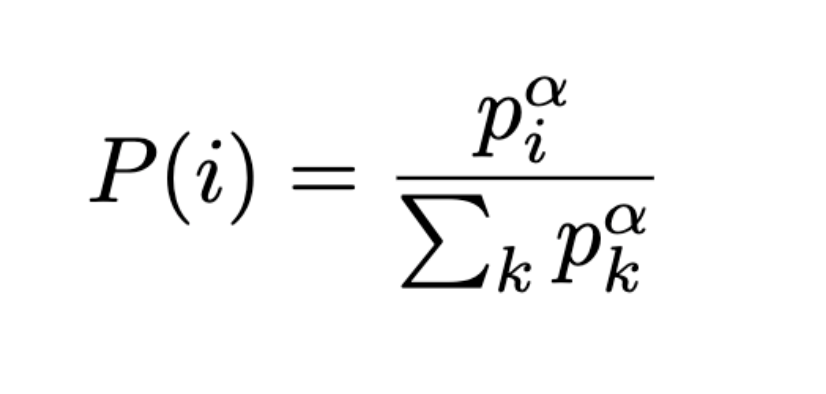

其中p(i)為第i個transition的priority，α為調節程度，α=0代表全部都平均採樣。兩個方案的差別在於priority。

結語

好哩理論跟公式今天講完哩，明天就來講程式跟其他細節的補充，我們明天見囉！