16 進制與 10 進制

什麼是進制?

進制其實就是指數字的每個位置所能容納的最大數字

比方說以我們最常見的十進制為例:

如果我們要表示 9 這個數字

可以直接寫出來

9

但是如果我們想將這個數字+1 該怎麼辦?
在十進制中我們並沒有可以表達 10 這個數字的符號,因此我們需要進位

10

如果我們想再對眼前這個數字+1
由於第一個項次已經變成 0 了,所以我們可以繼續往上加

11

現在讓我們轉換一下思路, 如果現在我們使用的是 2 進制呢?

那表示我們在數字的每的位置都只有兩個數字能夠來表達數值

如果我們想要在二進制寫出 2

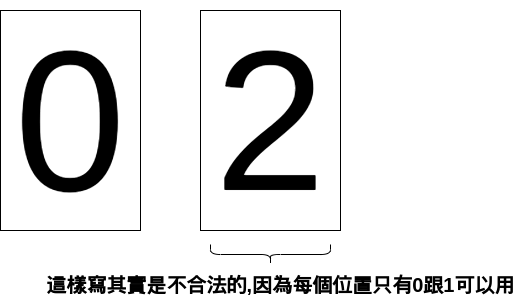
因此我們需要進位

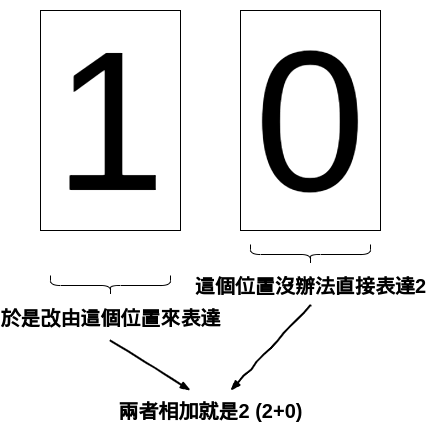
等一下,這個數字我怎麼看都是 10,怎麼會是 2 勒

這是由於現在我們所使用的表達方式跟我們常見的表達方式不同

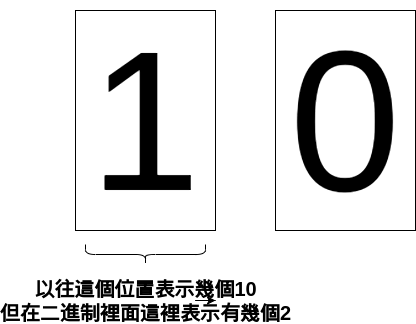
為什麼要這樣? 全部都使用 10 進制不是很好?

會使用 10 進制的理由是因為我們人有十根手指,所以當初發明數字的時候就使用了 10 進制
但是電腦只認得 0 跟 1,所以當然也只認得 2 進制

可以舉個現實生活中的例子嗎?

當然可以

• 你會說 5 點 61 分嗎?
  不會,因為你會把 60 分進位成一個小時變成 6 點 01 分

• 你會說 3 月 32 日嗎?
  不會,因為你會把 31 天進位成一個月變成四月一日

現在,讓我們來談談 16 進制

十六進制代表我們每個位置都有 16 個符號分別代表 0~15(總共 16 個數值)

在表達數字 0~9 的時候我們都可以直接寫出來,因為十進制跟十六進制的前十個符號基本是相同的
比方說我們現在寫個數字 9,十進制跟十六進制基本上都可以這樣表達

9

但是如果我們要對這個數字+1 呢?
十進制可以直接寫成數字 10

10

但是十六進制不行
因為在十六進制寫成 10 的話就會變成

等等,那如果我們要表達數值 10 該怎麼辦?

以下就是十進制跟十六進制的符號對照表

所以若是我們要在十六進制裡面表示 10 的話就只要寫下 A 即可

那為什麼要特地說 16 而不是 15,14 或 17?

理由是因為十六進制跟二進制的轉換是最方便的

所以當我們要轉換二進制時可以直接把二進制的數值四個一組分別寫出他們相對應的數值即可

• 1000111001011100

可以分成 1000 1110 0101 1100
再分別去找他們對應的數值

轉換完成就是 8E5C
是不是瞬間就短了許多?
相較之下如果剛才那串數字要轉成十進制就比較困難,需要去看每個位置的 0 跟 1 究竟代表多少

現在,讓我們來談談如何運算

因為上面就算列出了 8E5C 你依舊不知道這個數值究竟有多大

在對照表裡面只有列出 0~F,而 8E5C 很明顯大得多
所以我們必須做運算

看出規則了嗎?
其實跟十進位一樣每個位置都有各自代表的數值,只要將當前數值乘上當前位置所代表的數值即可

有了計算的概念我們就可以來寫我們的計算工具了
明天就可以開始動工我們的程式拉

延伸閱讀

• 想知道更多關於二進制與資料的關係可以看中山大學楊昌彪教授的影片

https://www.youtube.com/watch?v=b8wr9AUPDMM#t=1m9s