記錄學習內容。
主要是看網路上的文章和影片，做些紀錄。
內容可能有錯誤。

動態規劃

許多子問題非常相似，為此動態規劃法試圖僅僅解決每個子問題一次，從而減少計算量：一旦某個給定子問題的解已經算出，則將其記憶化儲存，以便下次需要同一個子問題解之時直接查表。

簡單來講就是 :
1 重複的事情只執行一次
2 存起來，下次用

找教學學習:
What Is Dynamic Programming and How To Use It

1
動態規劃 Dynamic Programming(簡稱DP） 可以用來替換遞迴 。

步驟 : 想遞迴解法 -- > 發現遞迴很多重複的部分 -- > 用陣列 把重複的部分存起來 -- > 遞迴通常 是 5 ->4 ->3 ->2 ->1 的 方式 稱為 top-down
。換成一般的迴圈 通常是 1 ->2 -> 3 - > 4 - > 5 稱為 bottom-up

2
費氏數列（Fibonacci）
費氏數列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
第0項: 0
第1項: 1
第2項: 前兩項相加

接著就解釋了程式 從遞迴 -- > 存東西 -- > 變迴圈

遞迴的時間複雜度是2的n次方 。 這邊不太懂 ，可能因為是
每一項都要在 往下長兩個遞迴。
所以 n 項 ，就要長 (2* 2 * 2 *… )個遞迴
然後每個遞迴 都是常數項的時間複雜度1 ，所以 就是2的n次方
參考:
2.1.4 Recurrence Relation T(n)=2 T(n-1)+1 #4

3
存東西的程式寫法 ， 時間複雜度就變成 0(n) 了 。
因為每一項東西最多運算一次 ，像是費氏數列第5項 ，有5個數字，所以總共5次 。

4
存東西的方法，還是遞迴。
我猜可能是因為10000 跑到 2 ，存太多 function 在記憶體了 。
所以有 maximum recursion depth exceeded in comparison 錯誤: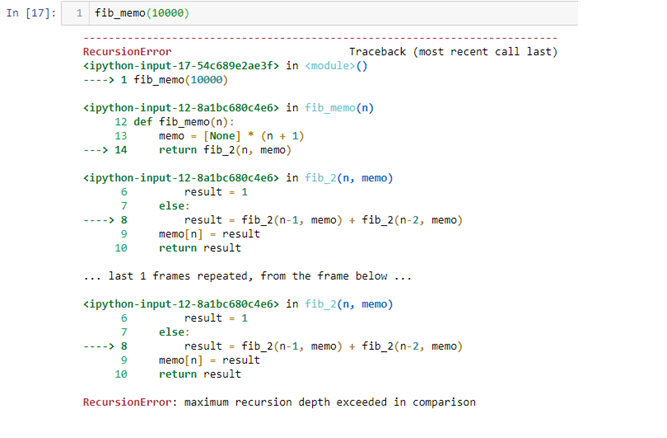

5
費氏數列只看結果的話 ， 還可以把陣列換成兩個數字就可以了 。
這樣空間複雜度原本是O(n) ， 就會變成O(1)

def fib_bottom_up_ab(n):
    if n == 1 or n == 2:
        return 1
    a = 1
    b = 1
    for i in range(3, n+1):
        a, b = b, a + b
    return b

其他問題

1 Rod Cutting

Rod Cutting - Dynamic Programming
https://www.youtube.com/watch?v=ElFrskby_7M&ab_channel=CSBreakdown

Cutting a Rod | DP-13
https://www.geeksforgeeks.org/cutting-a-rod-dp-13/

繩子每段長度的價格都不同。長度4的繩子的價格可以是
1+1+1+1 或是2+2 或是3+1 或是 4 。
dp 的方法是 多一個表格 紀錄 每段的最高價格 。
現在要找 4 的最高價格 ， 就是去 看這四個值 哪個最大:

長度3的最高價格 + 1的價值
長度2的最高價格 + 2的價值
長度1的最高價格 + 3的價值
4的價值

2 Longest Palindromic Subsequence

Longest Palindromic Subsequence | DP-12
https://www.geeksforgeeks.org/longest-palindromic-subsequence-dp-12/

Longest Palindromic Subsequence | Dynamic Programming | Set 12 | GeeksforGeeks
https://www.youtube.com/watch?v=TLaGwTnd3HY&feature=emb_logo&ab_channel=GeeksforGeeks

在一個字串中 找 最長的Palindromic Subsequence

ABCBA 就是 Palindromic Subsequence 。因為 從左到右唸 跟 從右到左唸 一樣 。
或是是 以C 為對稱軸 ，會一樣 。

BCB 是 Palindromic Subsequence ，然後A等於A ，那ABCBA 也是Palindromic Subsequence 。

3 Johnson’s Algorithm

Johnson’s Algorithm
https://medium.com/algorithm-solving/johnsons-algorithm-c461506fccae

任兩點之間的最短路徑-Johnson's algorithm
https://www.youtube.com/watch?v=hl3cgWwJS7I&ab_channel=%E6%B4%AA%C3%82ng%E6%98%A5%E7%94%B7Chhun-L%C3%A2m

Dijkstra 不能處理有負邊的情況 ， 所以 想辦法讓長度 都 >=0 ，就可以繼續用Dijkstra 了。

Johnson’s Algorithm 一開始 先讓 起點 增加 連到所有點 的路徑 。
然後用 Bellman-Ford 找到 起點 到 所有點的最短路徑 。

然後 E(a,b)邊的路徑，經過+h(a)-h(b)的調整後，都能夠變為非負路徑。

都變為非負路徑之後 ，再繼續Dijkstra 。
最後在 +h(b)-h(a) 復原路徑