記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
還不太了解，內容可能有錯誤。

Leetcode 1192. Critical Connections in a Network

筆記:

1 圖有 點 和 邊

假設有一個點是3
另一個點是4

邊的表示方法就是[3、4]
代表3 到 4

如果是 undirected graph (沒方向(箭頭)的圖)
[3、4] 就代表 3到4 、 4到3都可以 。

這題是undirected graph。

2

題目 給 connections = [[0,1],[1,2],[2,0],[1,3]]
代表 0 1之間相連 、1,2之間相連 、2,0之間相連 、1,3之間相連
有4個邊(edge )

3

有一種邊 叫做 critical connection 。
這種邊 移除 後 ， 會讓1個 圖 變成 兩個圖 ， 就會讓 某些點 到 不了 某些點
如圖 ，這條紅色的邊 就叫做critical connection 。

教學來源:
Critical Connections in a Network - Leet Code Hard Problem

影片解題筆記:

1

List<List> connections 代表 題目給的邊:
connections = [[0,1],[1,2],[2,0],[1,3]]

2

ArrayList[] 就是 [ArrayList , ArrayList, ArrayList, ArrayList ]
陣列裡面放 ArrayList 資料。

3

先把[[0,1],[1,2],[2,0],[1,3]] 換成
[ (1,2) ,(0,2,3), (1,0), (1) ]

代表 0 跟 1,2 這二點 有邊
1 跟 0,2,3 這三點 有邊
2 跟 1,0 這兩點 有邊
3 跟 1, 這一點 有邊

4

接著dfs 走訪 圖 ，先看每個變數是什麼意思:

ArrayList<Integer>[] graph  : [ (1,2)  (0,2,3)  (1,0)  (1)  ] 代表圖

int currentNode : 現在的點

int parentNode : 上一個走過的點 ，像是A點 走到 B點  ，A點就是 parentNode ， B點就是 currentNode

int[] times : 存每個點 是 第幾個走到的

int[] lowTimes : 如果這個點有Back edge：(所有指向ancestor()的edge)
，會更新lowTimes，讓lowTimes 跟 鄰居(祖先) 有一樣的lowTimes

boolean[] visitedNodes : 節點拜訪過了沒? True代表走過了

List<List<Integer>> ans :  最後的答案 ，代表有哪些邊是critical connection 。

關於Back edge:

參考:
Graph: Depth-First Search(DFS，深度優先搜尋)

0走到2在走到1，1又可以走到 0 。 1走到0 就叫做Back edge。

代表 有 2 這個點的邊 ，不會是 critical connection 。
因為拿掉2 ，1 和 0 還是可以連接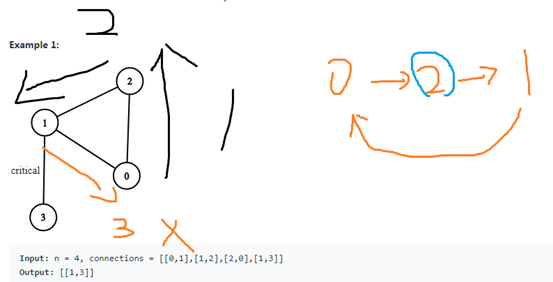

來看DFS內的程式順序:

題目的圖 :[ (1,2) (0,2,3) (1,0) (1) ]

一

0 點 先 走到 1 點

1 點 是 (0,2,3) ， 先走到0點 ，但是0 點是上一個走過的點 ， 所以略過。
所以走到2點

2點 是 (1,0) ，所以走到1點 ，1點是上一個走過的點， 所以略過。
接著走到0 點 ， 0拜訪過了 ，所以執行這段程式:

lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]);

也就是:

Math.min(lowTimes[2], lowTimes[0]) -- >
Math.min(2, 0) -- >
0

所以2 點 的lowTime 會被更新為0

Time 的意思 應該是 第幾個走到。
lowTimes 則是有考慮到backEdge的狀況 ，lowTimes要用來判斷是不是Critical Connections 。
所以現在2的 time為2 ， lowTimes為0 。

不太懂，總之繼續執行程式 :
2 這個點就算完成遞迴了
所以我們退回1 這個點 ， 1會執行dfs的下一行:

dfs(graph, neighbourNode, currentNode, times, lowTimes, visitedNodes, ans);
lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]);
if (times[currentNode] < lowTimes[neighbourNode]) {
    ans.add(Arrays.asList(currentNode, neighbourNode));
}

lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]); 
也就是Math.min(lowTimes[1], lowTimes[2]);
也就是Math.min(1, 0);
也就是0


接著if (times[currentNode] < lowTimes[neighbourNode]) 
也就是 if (times[1] < lowTimes[2])
也就是 if (1 < 0)

接著繼續迴圈1走到3
3 沒有鄰居了，所以結束。

###　回到1 ，1繼續執行dfs 的下一行 :

lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]);
if (times[currentNode] < lowTimes[neighbourNode]) {
    ans.add(Arrays.asList(currentNode, neighbourNode));
}

lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]);
也就是 Math.min(lowTimes[1], lowTimes[3]);
也就是 Math.min(0, 3);
也就是 0

接著

if (times[currentNode] < lowTimes[neighbourNode]) {
    ans.add(Arrays.asList(currentNode, neighbourNode));
}
也就是if (times[1] < lowTimes[3]) 
也就是  if (1 < 3)
    ans.add(1 和3 這個邊);  答案就是1到3

1 也跑完遞迴了 ，所以接著回到0， 0接著到2，2 走過了 ，在判斷 一下２，再判斷一下０，程式就結束了
流程大概懂了 ，但是沒有說很熟，就先到這吧

程式改成這樣　，可以印出來測試：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class Solution {

    private static int currentTime = 0;

    public static List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
        {
            int[] times = new int[n];
            int[] lowTimes = new int[n];
            boolean[] visitedNodes = new boolean[n];
            List<List<Integer>> ans = new ArrayList<>();

            ArrayList<Integer>[] graph = new ArrayList[n];
            for(int i = 0; i < graph.length; i++) {
                graph[i] = new ArrayList<Integer>();
            }
            for(List<Integer> connection: connections) {
                graph[connection.get(0)].add(connection.get(1));
                graph[connection.get(1)].add(connection.get(0));
            }
            for (int i = 0; i < n; i++) {
                visitedNodes[i] = false;
            }

            //看一下graph[i]的內容
            //確定是[ (1,2)  (0,2,3)  (1,0)  (1)  ]
            for (int i = 0; i < n; i++) {
                System.out.println("graph[i]?"+graph[i]);
            }

            dfs(graph, 0, -1, times, lowTimes, visitedNodes, ans);
            return ans;
        }
    }

    private static void dfs(ArrayList<Integer>[] graph, int currentNode, int parentNode, int[] times, int[] lowTimes, boolean[] visitedNodes, List<List<Integer>> ans) {
        System.out.println("currentNode?"+currentNode); // 0 1 2 3
        visitedNodes[currentNode] = true;
        times[currentNode] = lowTimes[currentNode] = currentTime++;
        System.out.println(currentNode +"  currentNode --  >  " + (currentTime-1)); //因為前面＋＋了，所以－１觀察

        for (int neighbourNode : graph[currentNode]) {
            if (neighbourNode == parentNode)
                continue;
            else if (!visitedNodes[neighbourNode]) {
                dfs(graph, neighbourNode, currentNode, times, lowTimes, visitedNodes, ans);
                lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]);
                if (times[currentNode] < lowTimes[neighbourNode]) {
                    ans.add(Arrays.asList(currentNode, neighbourNode));
                }
            } else {
                System.out.println("lowTimes[currentNode]?"+lowTimes[currentNode]);
                System.out.println("lowTimes[neighbourNode]?"+lowTimes[neighbourNode]);
                lowTimes[currentNode] = Math.min(lowTimes[currentNode], lowTimes[neighbourNode]);

            }
        }
    }

}


public class GraphTest {
    public static void main(String[] argv) {
        List<List<Integer>> connections = new ArrayList<>();
        List<Integer> edge = new ArrayList<>();
        List<Integer> edge1 = new ArrayList<>();
        List<Integer> edge2 = new ArrayList<>();
        List<Integer> edge3 = new ArrayList<>();
        edge.add(0);
        edge.add(1);

        edge1.add(1);
        edge1.add(2);

        edge2.add(2);
        edge2.add(0);

        edge3.add(1);
        edge3.add(3);

        connections.add(edge);
        connections.add(edge1);
        connections.add(edge2);
        connections.add(edge3);
        System.out.println(connections); //[[0, 1], [1, 2], [2, 0], [1, 3]]

        List<List<Integer>> ans = Solution.criticalConnections(4, connections);
        System.out.println(ans); //[[1, 3]]
    }
}