在我們的日常生活和工作中，經常會遇到許多包含不確定結果的現象。例如，股票的價格是要上漲、下跌或者平盤？已經布滿烏雲的天空是否下雨？某項工程是否能夠按期完工？投資項目盈利可能性多大？等等。

上述這些現象都有兩個特點：

事先不能確定哪一個結果出現；

各種結果在多次重複過程中體現出某種統計學規律；

這類現象就稱為不確定現象，或者稱為隨機現象。因此，我們使用一個數值來度量隨機現象中某一結果出現可能性的大小，這個數值就被稱為機率。機率的取值總是在0到1之間。機率值等於0表明該現象不可能發生；機率值等於1表明該現象必然發生；介於0和1之間的機率則說明該現象出現可能性的不同程度。

幾種機率定義中的短語解釋

試驗：試驗就是指可以產生明確結果的過程，這個結果可以是定量的，也可以是定性的，但每一次試驗只能有且只有一個結果發生。

樣本空間：當一次試驗所有可能的結果都確定時，我們就說確定了該試驗的樣本空間，即所有可能試驗結果的集合稱為樣本空間。

樣本點：樣本空間中每一個試驗的結果稱為一個樣本點。

事件：每一個樣本空間都包含著許多結果，一般稱這些結果為事件。

簡單事件（基本事件）和複合事件：只包含一個樣本點的事件稱為簡單事件或基本事件。包含多個結果的事件稱為複合事件。

確定機率的兩種主要方法：

古典法

古典法機率又叫做事前機率，即如果每一基本事件出現的機率是等可能的，則不需要做任何試驗就可以事前計算出事件的機率。其計算方法為：

相對頻數法

相對頻數法是用過去發生的事件的相對頻率當作機率。這種機率也可以叫做預計機率。使用相對頻數發確定機率的問題是，人們常常無法獲得所需要的重複試驗的次數。例如在投擲硬幣的試驗中，投擲次數越多，相對頻率就越穩定在0.5左右。就是說，採用相對頻數確定機率時，通過增加試驗次數，就能提高機率精確性。其計算方法為：

機率的事件中，存在以下幾種關係

事件的補。事件A的補就是所有在樣本空間S內但不包括在A內的所有樣本點的集合。

兩事件的並。屬於事件A或屬於事件B或同事屬於事件A和B的樣本點組成的集合。

兩事件的交。同事屬於事件A和事件B的樣本點的集合。

互斥事件。如果事件A發生，則事件B就不發生；或者事件B發生，事件A就不發生，則事件A與事件B互斥。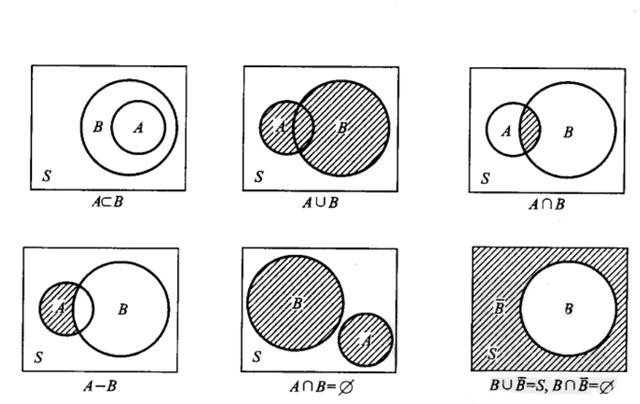

機率的運算

加法公式。加法公式用來計算事件A發生或B發生或者同時發生的機率，公式如下：

條件機率計算。如果有兩事件A與B，在B已經發生的條件下，A發生的機率即為A的條件機率，表示為：

讀作「給定B下A的機率」，其公式如下：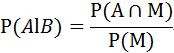

乘法公式。乘法公式是用來計算兩事件交的機率，其計算公式如下：