記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
以下內容大多來自網路上大大們的文章。截圖也來自文章和影片。
還不了解，內容可能有錯誤。

圖有很多 最短路徑的演算法 。

從某個點 到 其他全部點的 最短路徑 。
或是 某個點 到 終點的 最短路徑
之類的問題。

每個邊 都有 1 個變數 : weight， 代表這條路的距離 。

這類問題就是 找到 一些邊 (路) ，這些邊相加起來的weight要是最小值(代表最短路徑)

先從Floyd-Warshall開始看
All Pairs Shortest Path (Floyd-Warshall) - Dynamic Programming

筆記:
Floyd-Warshall演算法

Floyd-Warshall中文亦稱 弗洛伊德演算法

可以正確處理有向圖或負權（但不可存在負權迴路）的最短路徑問題

什麼是負權迴路(Negative Cycles)?

Floyd Warshall All Pairs Shortest Path Algorithm | Graph Theory | Dynamic Programming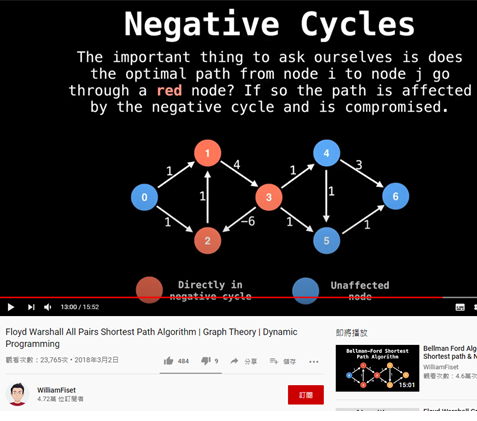

1、3、2所圍成的圈圈 ，就叫做負權迴路(Negative Cycles) 。
今天要1到 1 的話 ，原本是0
，但是現在 可以 1 --> 3 -- >2 -- >1 = -1
所以判斷負權迴路(Negative Cycles)的方法就是:自己到自己變成負數

複雜度

> Floyd-Warshall演算法的原理是動態規劃

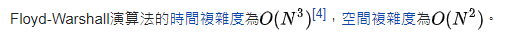
因為是迴圈 加上 陣列(存檔空間)

接著來看:
3.6 Dijkstra Algorithm - Single Source Shortest Path - Greedy Method
[演算法] 最短路徑 (Dijkstra 演算法)

Dijkstra Algorithm。主要內容是指定一個點 (源點) 到其餘各個頂點的最短路徑，也稱作「單源最短路徑」。

Dijkstra Algorithm 在邊長是 負數 的情況下，答案可能會是錯誤的。

像是現在從1出發 ， 會先選 1 到 2邊長。
接著選 1 到 4 邊長。
接著選 4 到 3邊長 。
這時後就會發現 1 到 4 到 3 到2的距離是 -3 。
但是 用Dijkstra Algorithm 的方式 ，1 到 2 的最短距離是 3，所以答案錯誤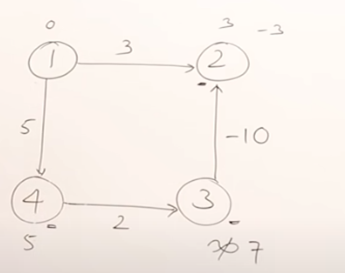

看一下維基的時間複雜度:
戴克斯特拉演算法
目前學的是第一種 。 其餘的都不會:

接著來看離散數學教學的Dijkstra Algorithm:
[Discrete Mathematics] Dijkstra's Algorithm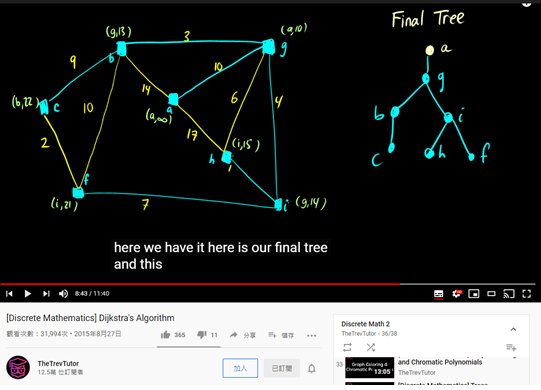

Dijkstra's Algorithm (戴克斯特拉演算法)
這個演算法 ，代表 某個點(a) 到 所有其他點(除了a以外) 的 最短路徑 。

一開始 先從 a點 開始檢查 ，與a相鄰的 就寫 數字長度 ，
與a不相鄰，代表走不到，所以寫無窮遠 。

a檢查完(觀察完)所有點後，看哪個點與a最近，發現g最近
，就代表走a -- > g 這條路 。

下一輪 再從 g開始檢查 。像是圖中 g到b 是13 ，發現比原本14還少。
所以從(a,14)改成(g,13) 。

g檢查完所有的點後 ，發現 b最近 。
路徑就變成a -- > g -- > b

接著就是 b檢查
，b檢查完所有點後 ，發現i最近
路徑變成a -- > g -- > b -- > i

這邊發現這樣寫很奇怪 。因為b走不到i ，

所以這個演算法 ，不是一個點接著一個點走的。
而是 一個點檢查、檢查完後，選擇目前最短的點 ，再繼續最短的點檢查…
直到所有點都跑完。

最後的結果 會顯示 a 到 所有其他點 的 最小長度 。
然後會形成一個樹 ，這個樹叫做Minimum Spanning Tree(MST，最小生成樹)

MST，最小生成樹 :

在一個圖中如果選了全部的點，而這全部的點又相連 ，然後是一個樹，就叫做Spanning Tree，
這些Spanning Tree 中，有些樹weight總和是最小的 ，這些樹就是Minimum Spanning Tree

關於Minimum Spanning Tree最小生成數:
Minimum Spanning Tree：Intro(簡介)

Dijkstra's Algorithm (戴克斯特拉演算法)
這個演算法 ，代表 某個點(a) 到 所有其他點(除了a以外) 的 最短路徑 。
所以 好像不一定是Minimum Spanning Tree(MST，最小生成樹)
不一定 會 是 weight總和是最小的