記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
以下內容大多來自網路上大大們的文章。截圖也來自文章和影片。
還不了解，內容可能有錯誤。

這四篇教學交錯看。

教學來源:
輕鬆談演算法的複雜度分界：什麼是P, NP, NP-Complete, NP-Hard問題

論P,NP,NP-hard,NP-complete問題

8. NP-Hard and NP-Complete Problems

8.1 NP-Hard Graph Problem - Clique Decision Problem

時間複雜度 是 O(2的n次方) 的演算法 。速度都很慢，像是河內塔 。

假設有30個盤子 。 2的30次方 會是
1,073,741,824 (10個數字)

假設有64個盤子 。 2的64次方 會是
18,446,744,073,709,551,616 (20個數字)

假設有1000個盤子 。 2的1000次方 會是
1.07150860718626732094842504906e+301
(不知道這個數是什麼)

NP是 non-deterministic polynomial-time
Ｐ是 polynomial-time (多項式時間)
多項式 就是 我們的 n (資料個數)，是在底下，不是在指數 。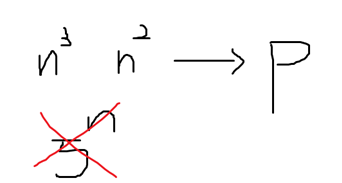

時間複雜度 是 O(2的n次方) 的演算法 ，都叫做
NP( non-deterministic polynomial-time ) ?

這樣想可能是錯的 :
文章中有講 世界上可以分為這四個問題:

NP定義:

non-deterministic polynomial-time 意思想成
時間複雜度 是 O(2的n次方) 的演算法 ，
雖然 我們 沒辦法 在 多項式時間 內完成 。
但是 我們 要假設 未來 某天 有人可以發明出在 多項式時間 內完成的方法 。
所以才叫做:
NP( non-deterministic polynomial-time )
不確定 的 多項式時間 。
只是不確定 ， 不是 {不可能}

影片教學裡有講 ， non-deterministic polynomial-time 包住 polynomial-time
P 想成 地球
NP 想成 宇宙
NP 以外的問題 想成 宇宙以外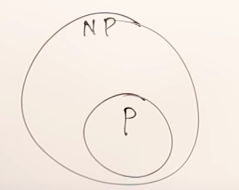

回到文章:

假設給予一組集合{−7,−3,−2,5,8}，問是否有一組子集合相加為0，怎麼做呢？

列舉出所有可能，每個數字都是要選或是不選 ，跟0/1背包問題一樣。

-7 + -3 + -2  + 5  + 8
-7 + -3 + -2  + 5  
-7 + -3 + -2  
…

所以有2 * 2 * 2 * 2 * 2 種可能 ， 2的n次方種可能 。
然後每一項 都要 相加 確認 是不是0 。
所以時間複雜度 會變成 O(N×(2的N次方))

但是今天我直接給你子集合(-3 、 -2 、 5)，問你是否相加為0 。
只要-3 + -2 +5 = 0 ，時間複雜度O(n) 就可以驗證答案是正確的了 。

所以

NP( non-deterministic polynomial-time ) 的意思:
不只是 (不確定的多項式時間)。
也是 (一旦有一個解 ， 可以 驗證這個解 在多項式時間內 完成)

所以 子集合加總問題 就是 NP問題

來看這部教學:

8.1 NP-Hard Graph Problem - Clique Decision Problem

什麼是 complete Graph ?

就是 每個點都要連到其餘所有的點 。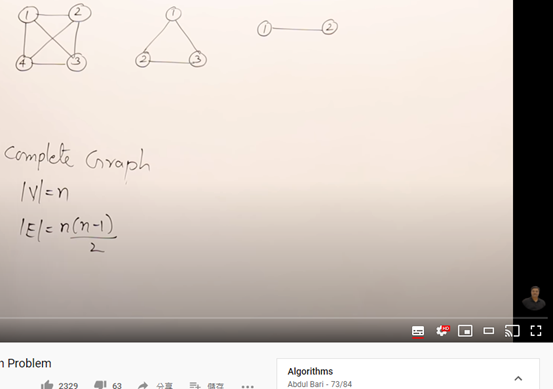

分團問題

分團問題

分團問題（clique problem）是問:

任意挑出k個點，我們可以簡單的判斷出這k個點是不是一個團

什麼是團 ? 就是 一個Graph，裡面 有一塊 是complete graph
如圖 ， 125 就是complete graph ，所以是clique

什麼叫做Decision Problem ?

有沒有、是不是的問題。
像是 : 這個圖中有沒有 三個點 的團 ?

要怎麼解這個問題 ? 要判斷幾次？
圖中有6個點 ，要選擇3個點 來檢查 ，這三個點視為一體 。
所以要判斷
6 * 5 * 4　/ 3 * 2 次
( 6個點挑3個點 ) / (因為3個點視為一體 ，不排序 ，所以3 * 2) 。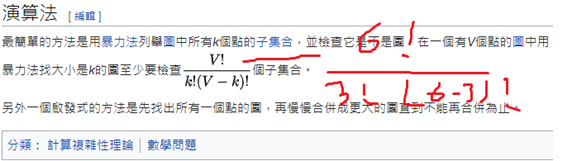

教學有證明clique problem 是NP-Hard Problem 看不懂 。

來看NP-Complete問題是什麼????

只要滿足以下兩個條件的，我們都稱之為NP-Complete：
1.「問題」本身是一個NP問題
2.所有的NP問題都可以用DTM在 polynomial time 內化約成為這個「問題」。

就是說 我們有很多的問題，時間複雜度都是2的n次方 。

我們要把這一堆問題 ，換成 另一個問題 。

如果在多項式時間以內 完成-- >這一堆問題 ，換成 另一個問題 。加上 這另一個問題本身也是NP問題

則這 另一個問題 稱為NP-Complete 問題 。

那什麼是NP-Hard 問題??

NP-Complete問題 本身是NP問題 ；
但是NP-Hard 問題 本身可以 不是 NP問題

文章中的這張圖很清楚:
左邊就是前面理解的範圍 。

右邊是P＝NP的情形。
如何讓P＝NP ?
我們要找一個NP-Complete 問題 ，這個NP-Complete 問題如果是 p問題，
，那所有的NP問題 都可以 變成 這個NP-Complete 問題 ，這個NP-Complete 問題 就是P問題啊! 所以全部都變成 P問題了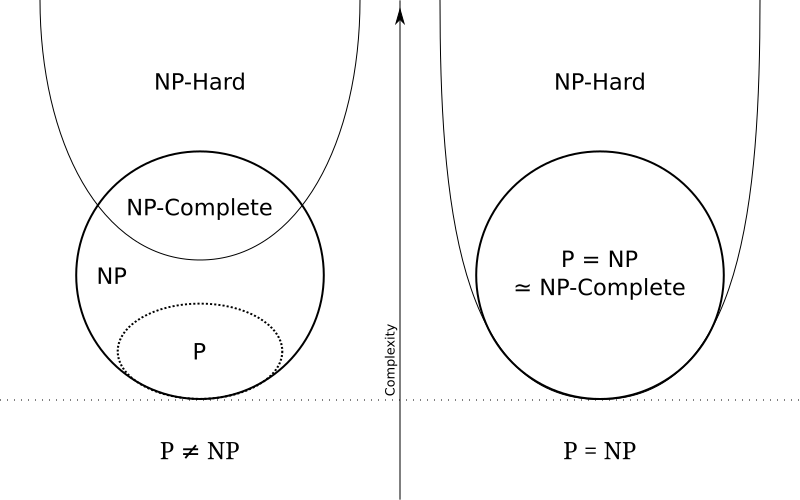

之後有看這兩系列教學:

【杰哥數位教室】演算法課程
https://www.youtube.com/playlist?list=PLpbuzGqDFzkj3DMCryCdgWQ1FwpgnMpR6

2019 Fall 台大資工 演算法設計與分析 NTU CSIE ADA
https://www.youtube.com/playlist?list=PLOAQYZPRn2V5C4Cx5tSLW8z0saWUm8LD-