[DAY 12] CNN 簡介

12th鐵人賽

zivzhong

2020-09-27 23:59:13

3493 瀏覽

分享至

前言

總算開始了一個跟DL比較有關係的名詞啦(?)一直以來科學家總想模仿動物的大腦來做AI結構，所以或多或少你們會看過科學家研究貓的腦部來知道大腦的哪個部分是做甚麼的，像下面這張圖，以期能夠設計出一套厲害的AI系統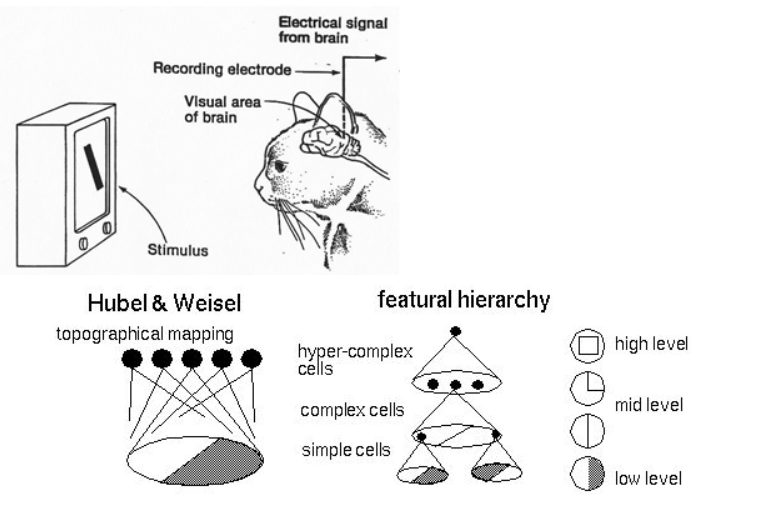

CNN做為DL崛起有著不可抹滅的功勞，像是拿到與紐約大學教授勒昆（Yann LeCun）和蒙特婁大學教授班吉歐（Yoshua Bengio）一起共同拿到 2019 圖靈獎的多倫多大學電腦科學教授辛頓（Geoffrey Hinton）在 2012 的 ImageNet 競賽提出的 AlexNet 以驚人的優勢贏了比賽。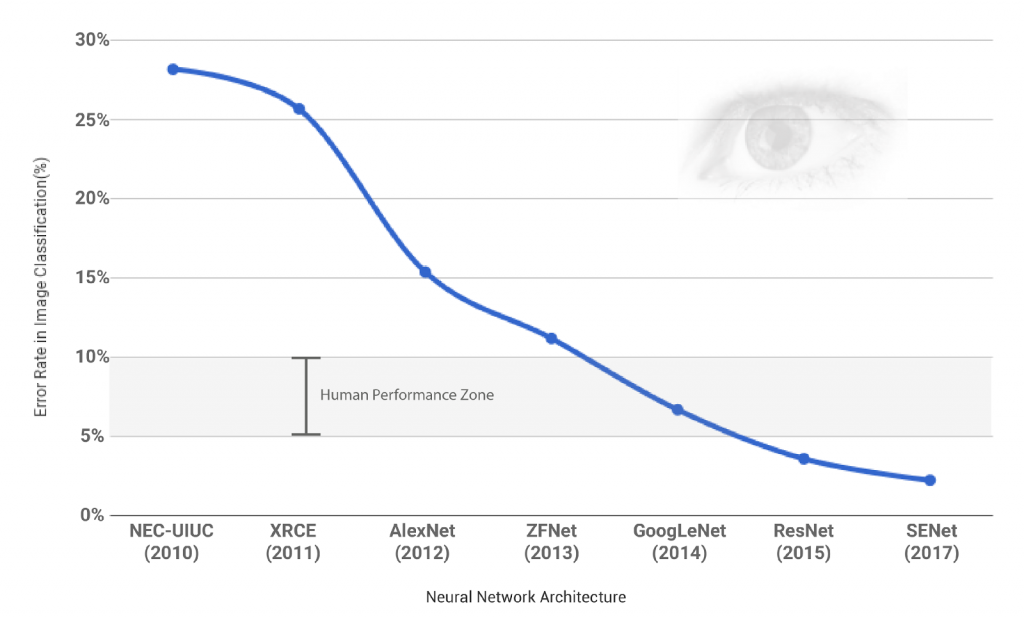

我們可以看到2012提出的 AlexNet相對於之前非 CNN-based 方法有了個非常大的進步，而之後提出的方法也是CNN-based 的，並且到了 2014 的 GoogleNet 電腦視覺的辨識能力就已經跟人類差不多了，而 ILSVRC 的classification比賽在2017年也是最後一屆，因為之後提出來的model的辨識能力已經遠遠超過人類的，這也說明了 CNN 的powerful !!

CNN

由於 CNN 的內容眾多並且也是各類型的 model (VAE、GAN)的基礎或者子結構，因此我們會花比較多的篇幅來說一下，主要會分成以下幾點來說明:
1.簡介與背景
2.結構簡介
3.Convolution、Pooling等等算法
4.Backward 更新
5.實做以及實例演練

結構簡介

首先先舉一個簡單的CNN例子給大家看看，如下圖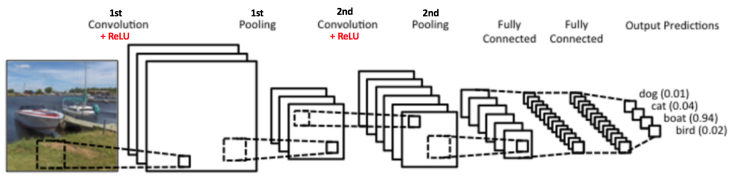

這是一個簡單的 CNN 使用例子，使用一個CNN做照片分類，我們可以看到這個CNN Model的 Input 是一張照片，中間一堆方格的意思表示著 CNN 的結構，最後輸出的是是個機率值，代表著這個model認為這張照片對這些類別的機率值，圖片中覺得這張照片最有可能是 "boat" 這個類別，因為他的機率最高(0.94)。
而這張圖片也充分提示了我們一個基本的 CNN model 會有的結構會有以下幾個:
1.Convolution Layer
2.Pooling Layer
3.Activation Function (圖片中紅字 "Relu" 的部分)
4.Fully Connected Layer
當然在CNN結構中其實也不只這一些小結構，也可以再加上像是 Batch Normaliztion 等等結構，但對於初不接觸我們先專心討論核心的結構就好，以下提點各種 Layer 的目的以及大概長啥樣:

Convolution Layer

不囉嗦先上張圖介紹 Convolution 在算的時候長啥樣

如果大家看不到上面這張這可以看下面這一張XD
Imgur
Convolution Layer 主要是用來從前一層的output中汲取 feature 或者資訊成為新的一張 feature map
那我們先從 Convolution layer 中的名子 convolution 介紹起

Convolution 計算

首先在 Convolution layer我們要提到我們最重要的計算模式 -- Convolution 計算 ，但這麼快直接跳進去我們大概會出事，所以我們先提一下幾個設定:
1.為求簡單，我們先設定我們的 Input 圖片為一張一個 channal 的2D 圖片，例如是一張灰階照片，而像是彩色RGB照片為 3 個 Channal 這樣。這張照片只有 5 * 5 大小，每個像素值只有0或1 (當然正常的灰階照片值域在0~255)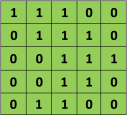

2.我們有一個filter(或者也稱為 kernal)，大小為 3 * 3，是用來與input進行 convolution 計算，得到我們的 feature map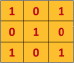

3. Feature map 為我們這個 convolution 計算的結果，上面內涵著我們從Input萃取出來的資訊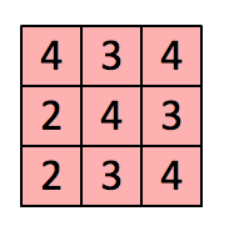

4. Convolution 計算規則如下:
依照定義，連續的2D convolution 計算規則如下: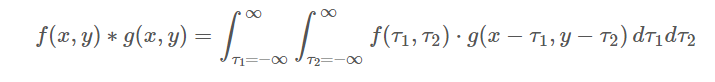

但我們今天是2D的一格一格進行convolution計算，因此是屬於離散的，所以也別慌，公式會像下面這樣: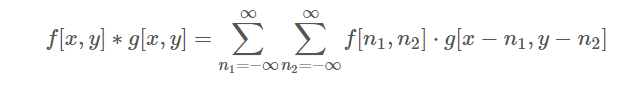

5. 在進行 Convolution 計算時，細心的你或許會發現，诶~我算完了這3 * 3 格Input與kernal的convolution之後，那下一輪要從哪裡開始算呢?是移動一格，還是移動整整三格不要重複算到已經算到的部分在開始算，這是可以介紹一個概念叫做 "Stride" 意思就是步幅，就是你這 Kernal 每次跟 Input 上的 3 * 3 算完之後往旁邊移動的像素數，當然我們可以直覺發現如果Stride越大，那Kernal跟Image做完整個 convolution 的次數越少，所產生的feature map越小，舉個例子齁: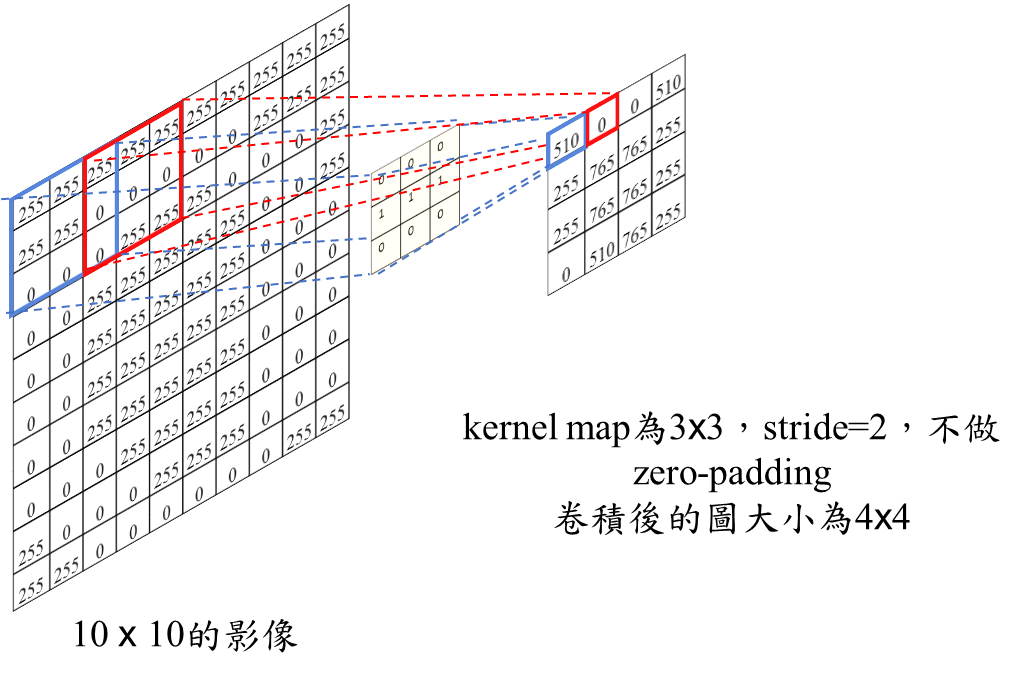

6. 诶诶，上面那張圖怎麼多了一個新名詞 "Padding" ，這又是啥QQQQ 細心的你或許想過，我們的 kernal 今天算到邊邊時，以 5 * 5 image 為例子，你的kernal中間已經移動到Image邊號為5的位置，阿這個不是不能算嗎?我們Image又沒有第6格可以給 kernal 做 convolution ，那怎麼辦QQQ旁邊補0或者啥的呀XDD "Padding" 就是定義在整個 Image外面我們要做甚麼處裡，常見的有 Zero-Padding(如下圖)，注意input最外圈填0的部分就是 padding加上去的，當然也有改成填1的paading方法: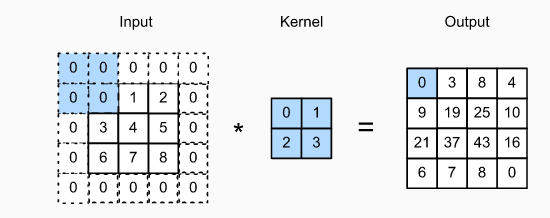

7. 結合上面的幾個的動圖整個convolution可以參考下面動圖:

如果大家看不到上面這張這可以看下面這一張XD
Imgur

Pooling Layer

Pooling Layer 也被稱為 Downsampling 、 Spatial Pooling）或 Subsampling，主要是可以縮小、濃縮 Feature map，但同時希望能夠保留 Feature map 內的關鍵訊息，即用來降低採樣數，可以控制所存著並丟到下一層的資訊不會越來越多，但又不會流失重要資訊效果就像是這個下面連結一樣:
Pooling效果參考
把一張照片擷取些小照片資訊拼起來，畫面變小但還是看得出來是啥
Pooling主要的效果有:

增加感受野，因為照片變小了，所以如果kernal在上面移動做計算，花更少的步數就可以看完整張照片
Translation Invariance：因為pooling對照片進行壓縮，所以已經抽象化並壓縮了一部分的資訊，像是 maxpooling 是取一定空間方格內的最大值，所以只要這個方格一起移動，那麼其實取 pooling 後的結果一樣會保留最大值的那格因此允許照片中的物體做一定量的移動
減小矩陣大小可以減少記憶體使用量以及減少了計算參數可以避免 Overfitting
常見的 Pooling有以下兩種 : Max 以及 Average，那麼顧名思義的效果也可見下面

5.如果有多張Feature Map，那Pooling是分別對每張 Feature Map 做!!

Activation Layer

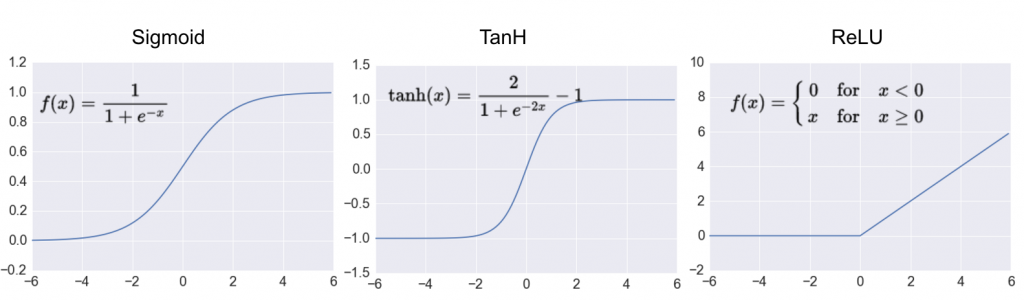
在每層 convolution layer 之後，讓output的值經過一個 non-linear 轉換，可以讓我們的 Model 去擬合更複雜、非線性的資料，常見的有像是 Relu、sigmoid等等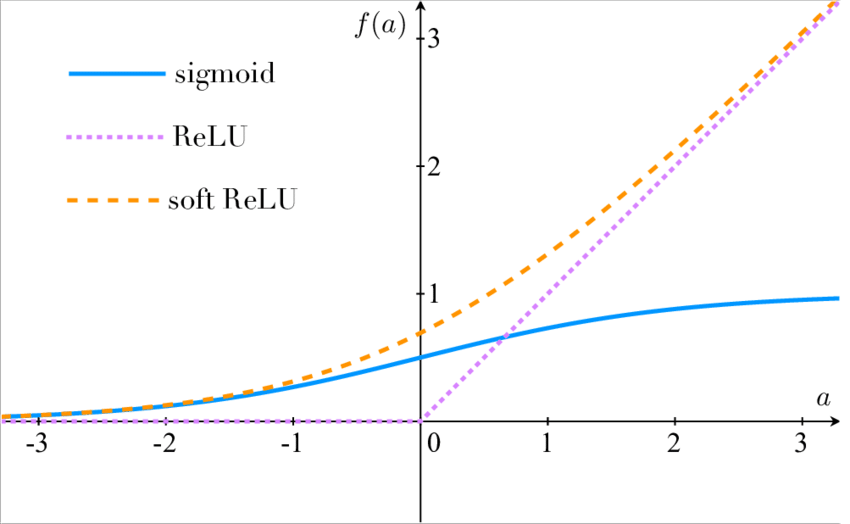

那在最開始的時候，科學家們參考了生物學界的神經在傳遞資訊給下一個神經元時會有全有全無律，意即如果不超過一定量值時，是不會傳遞資訊下去的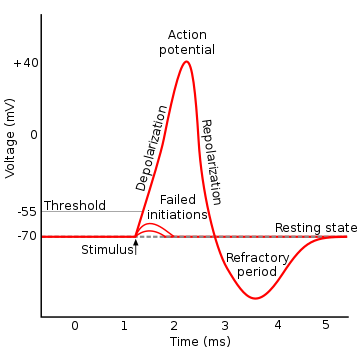

在類神經網路中使用Activation Function(激勵函數)，主要是利用非線性方程式，解決非線性的問題，若不使用激勵函數，類神經網路即是以線性的方式組合運算(意即多個矩陣相乘還是只是個矩陣)，而Activation Function其實可以隨意設計但有以下兩個限制:

激勵函數需選擇可微分之函數，因為在誤差反向傳遞(Back Propagation)運算時，需要進行一次微分計算。
2.在深度學習中，當隱藏層之層數過多時，激勵函數不可隨意選擇，因為會造成梯度消失(Vanishing Gradient)以及梯度爆炸(Exploding gradients)等問題。這兩個問題我們會在 "Backpropagation"那章提及
常見的 Activation Function 有以下幾個:

Fully Connected Layer

最後我們來提一下 fully connected layer，顧名思義他會與前一層的每個 unit做連結計算，因此所需要的記憶體通常不小，而convolution layer也是提出用來更有效、使用較少的變數達到一樣的計算擬合能力的 tool。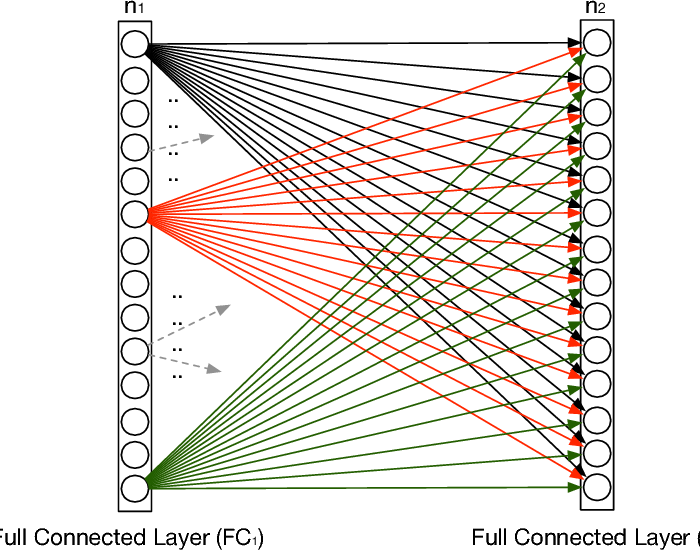

在整個 CNN model 中，如果說前面的 Convolution layer 是為了把 Feature 從Input Image中取出來，那麼通俗來說，Fully connected layer就是為了把萃取來的Feature 對映(Mapping) 到樣本Label的空間(Space)中做Classification，其本質上來說就是一個矩陣向量乘積:
$Y = Wx$
那行是大概如下:

OK，我們知道了 Fully Connected 是一個轉換矩陣去試著 Mapping feature Map 到 Label space，但這是可能會有個問題QQ那麼就是經過 Convolution 計算之後不是一個Feature map 長得是矩陣那種方形的嗎?怎麼就變成一條長的可以跟 Fully Connected做全連接了?????
這邊要介紹一個工具叫做 Flatten:

Flatten

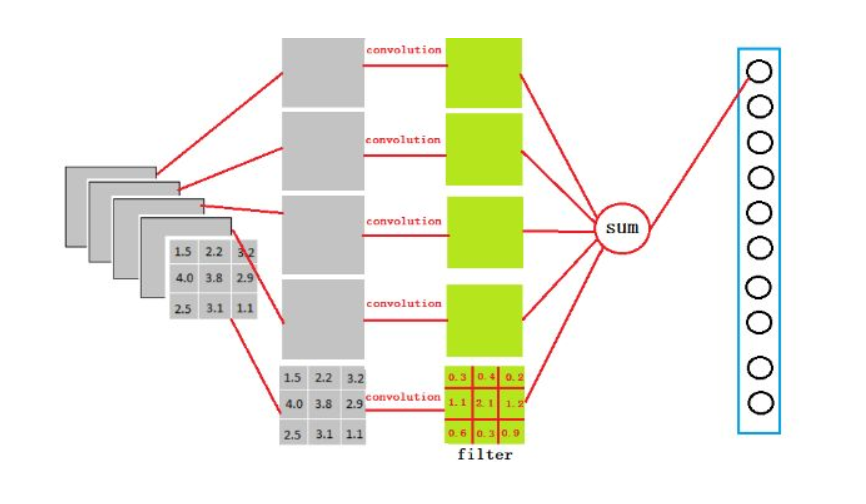
假設我們有5個3 * 3的Feature map，然後我們需要用讓他變成4096維然後跟Fully Connected layer 做連結，那麼其實Flatten此時就是 3x3x5x4096 的 convolution layer 去跟 feature map 做 convolution計算得出來，太繞口了嗎?那麼只需要記做下面這張圖就好: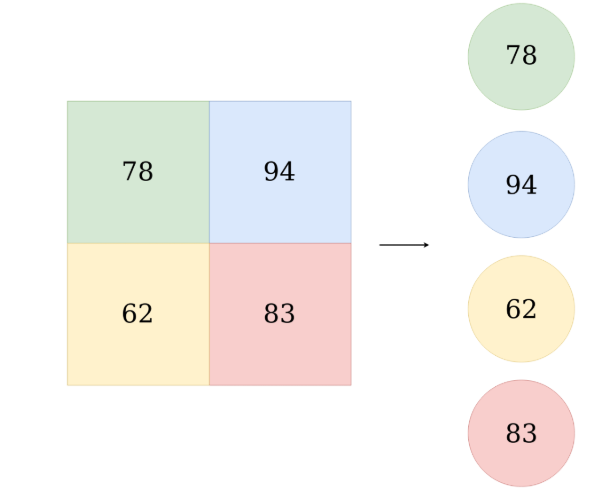

Loss Function

我們的 Model 總算測出來一個甚麼鬼了XD逾時我們可以去找別人開始吹我們的 Model有多猛，但我們需要一個量化的值去說明我們的 Model 有多好，或者換句話說，我們預測出來的值能跟 Ground Truth 有多像。所以這邊我們知道了第一個 Loss Fuction的重點也是最重要的一個重點 :
Loss Fuction 必須要能夠足夠有效地說明你的 Prediction 跟 Ground Truth有多像
所以其實 Loss Function 某種程度上也代表了我們希望我們的 Model 的 Goal，或者說我們想要縮小的、最小化的目標函式是甚麼(Objective Function)
那麼常見的用來做Classification的 Loss function就是交叉熵(cross-entropy)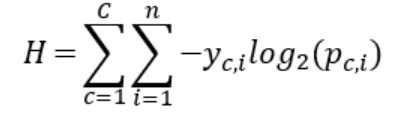

結語

作為 DL 的入門結構， CNN 的設計我們需要好好的去掌握，知道每個部分的計算以及用意，對於之後在建構較為複雜的Model 我們就能夠更大膽的把CNN的這個子結構當零件組上去!!有了這些工具，其實我們已經有能力可以構建出一個 CNN 模型，但這個雖然能動，卻還不具備學習的能力，因此下一章我們將介紹 CNN 進步的動力: Backpropagation !
加油!這是開始的一小步，但卻是堅定的一小步