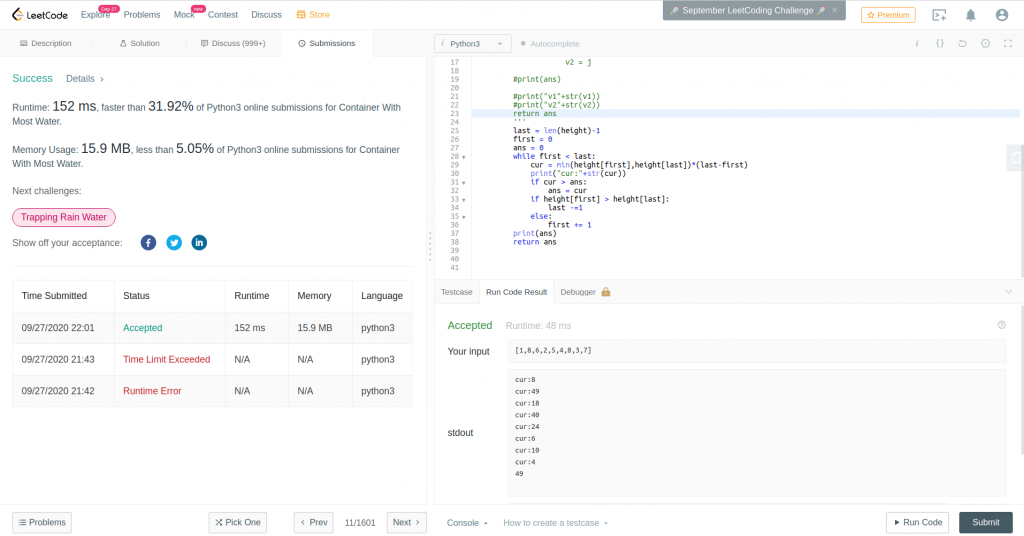
描述:
Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

相當有趣的一題

題意: 好幾根柱子 高高低低,選兩柱 中間裝水,問最大水量。

思路: 任選兩柱 以較矮柱為高，因此得

min(height[left],height[right])

那寬度呢？
不要忘記 我們要求的是 最大面積,所以越寬越好(也就是說兩柱離越遠越好),
但是呢 面積為 長x寬 而 長以矮的為主,所以阿 感覺是每一種組合都得試試~~

起初 是以 double for 來組,再取最大 ... 但是會超時 QQ

所以看了 GeeksforGeeks - Container with Most Water 的 Algorithm
遵循 Wait a day : 談談 寫程式技巧 寫了個 草稿大致怎麽做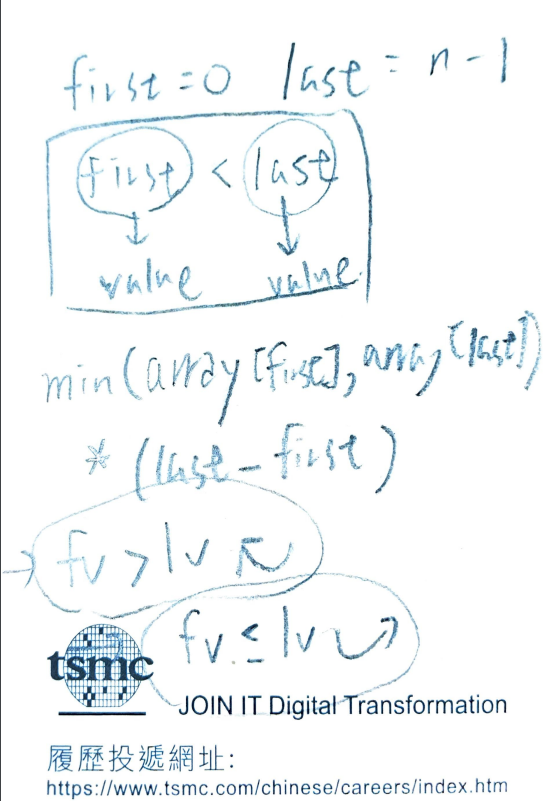

再想了一下,覺得那個 左右 移動很有道理 > 就是要找 較高的柱

左柱(左指針) 初始為 最左邊的那根
右柱(右指針) 初始為 最右邊的那根

如果 左柱 低於 右柱

左指針右移 找較高的柱

如果 右柱 低於 左柱

右指針左移 找較高的柱

過程中 紀錄目前面積最大的(在考慮兩柱取矮柱的條件下)
如果大於目前最大則更新,最後(左指針<右指針都跑完的情況)面積為所求。

正解

class Solution:
    def maxArea(self, height: List[int]) -> int:
        '''
        ans = 0 
        
        left = 0 
        right = (len(height)-1)
        
        for i in range(len(height)):
            for j in range(i+1,len(height)):
                #print(j)
                v = min(height[i],height[j])
                area = v*(j-i)
                if area > ans:
                    ans = area
                    v1 = i
                    v2 = j 
                     
        #print(ans)
        
        #print("v1"+str(v1))
        #print("v2"+str(v2))
        return ans
        '''
        last = len(height)-1
        first = 0
        ans = 0 
        while first < last:
            cur = min(height[first],height[last])*(last-first)
            print("cur:"+str(cur))
            if cur > ans:
                ans = cur
            if height[first] > height[last]:
                last -=1
            else:
                first += 1
        print(ans)
        return ans
            
        
        

PS: 註解為 TTL 時的 Code
Note: print 盡量拿掉 因為太多print 可能造成 Runtime Error

Result