(今日內容將有數學式，請謹慎服用)
今天要介紹的主角，可以說他是影響模型輸出結果以及訓練過程中最大的功臣
，損失函數的設計能決定絕大部分模型的好壞，也就是—
Loss Function(損失函數)

損失函數基本上可以分成兩個面向(分類和回歸)，都是希望「最小化」損失函數。

“蛤? 為啥要把她最小化? 阿最小化了能幹嘛?”

這就要從「損失」這東西說起了，在回歸的問題中，基本上我們做影像辨識希望的結果是越接近正確答案越好，最好你就給我百發百中，每題都對。

*我訓練出來的百發百中模型:

拿上圖舉例，假設我們希望的結果是「射中主角」，而那些彈道為預測的結果
。
損失就是為了達成射中主角這個目的，「需要將彈道偏移多少公分」。換句話說，也就是「預期效果與實際情況的誤差值」。

那麼將損失最小化，自然就能讓模型的準確率提高；雖然不能百發百中，可能中個90發也不錯。

y表示實際值，ŷ表示預測值。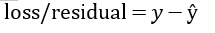

那麼在分類的問題中，就變成分類的錯誤率，當然理想情況是完美分類。

*我丟給模型的考題ヽ(́◕◞౪◟◕‵)ﾉ

y表示實際類別，ŷ表示預測類別。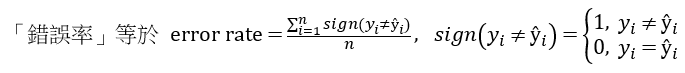

在分類的問題中，我們不會直接拿分類錯誤率當作損失函數進行最佳化，這就需要提到Cross-entropy，為求淺顯易懂，這裡只點出一些重點部分。

Entropy(熵) : 原本指的是科學中的雜亂程度。熵越高，越雜亂、越不確定；反之則越穩定、整齊。
EX : 假設今天某遊戲角色下次攻擊的暴擊機率為90%，那麼也就說明「下一次的攻擊很有可能會暴擊」。這樣就代表熵很低，下次的結果很穩定、確定。
那如果今天該角色的暴擊機率只有50%，那下次攻擊會暴擊的機會是一半一半，幾乎無法預測是否將會暴擊，那就是熵很高，結果充滿了不確定性。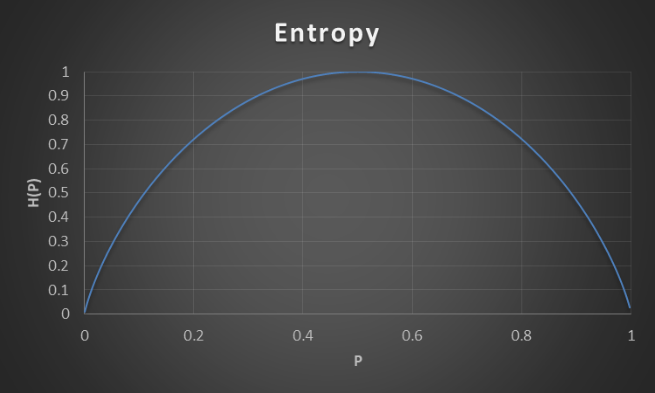

▲機率(X) 與 熵(Y)的分布圖

Cross Entropy(交叉熵) : 即為預測值與現實情況的誤差。現實與預測重複程度越高，交叉熵越低，結果越準確；若重複程度越小，則交叉熵越高，結果越不準確。

回歸常用的損失函數: 均方誤差(Mean square error，MSE)和平均絕對值誤差(Mean absolute error，MAE)

首先是均方誤差(Mean square error，MSE) : 通常預測與實際值的差有正有負，若直接相加，會變成100 + (-100) = 0 這種極為不合理的情況。

根本就是指蝶為鴿了吧 (X
若要避免這種情況，就必須讓所有差值變成正數，其中一個方法便是MSE:
用平方讓大家都變正
變正變大之後我們就是兄弟了 ♂

另一種方式為平均絕對值誤差(Mean absolute error，MAE) : 一樣是將誤差值轉正，用的是絕對值的方式。

這樣，Loss Function的部分算是重點介紹完了，下篇將會介紹Yolo的由來以及歷代的重大更新。

參考資料:
https://chih-sheng-huang821.medium.com/%E6%A9%9F%E5%99%A8-%E6%B7%B1%E5%BA%A6%E5%AD%B8%E7%BF%92-%E5%9F%BA%E7%A4%8E%E4%BB%8B%E7%B4%B9-%E6%90%8D%E5%A4%B1%E5%87%BD%E6%95%B8-loss-function-2dcac5ebb6cb
https://www.youtube.com/watch?v=uqYQ6pAdJ1A&ab_channel=%E6%84%9B%E7%94%9F%E6%B4%BB
https://r23456999.medium.com/%E4%BD%95%E8%AC%82-cross-entropy-%E4%BA%A4%E5%8F%89%E7%86%B5-b6d4cef9189d