圖是由節點(node)和邊(edge)所組成的，一個節點可能與多個節點相連著，而這些相連的節點又被稱作相鄰節點(neighbor)，圖在生活中應用的例子相當的普遍，像是人際關係的社交網路、尋找地圖最短路徑、通訊網路等等。

無向圖(Undirected Graph)

邊沒有方向性，A可以到B，B也可到A，概念類似雙向道，兩邊都可以通行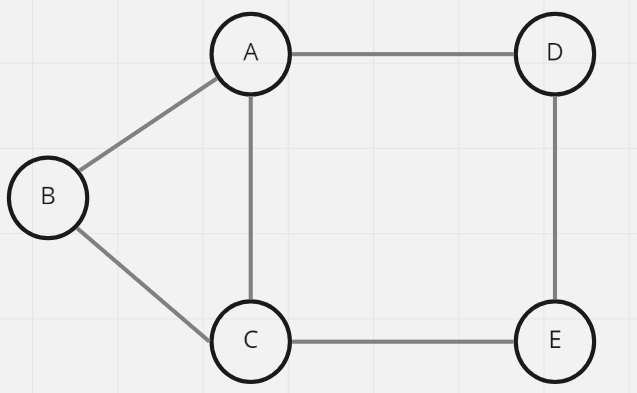

有向圖 ( Directed Graph)

邊具有方向性，B可以到A但是A不能到B，概念類似單行道，僅限單邊通行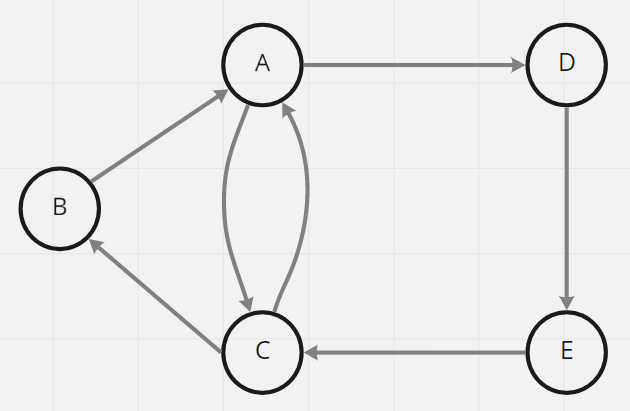

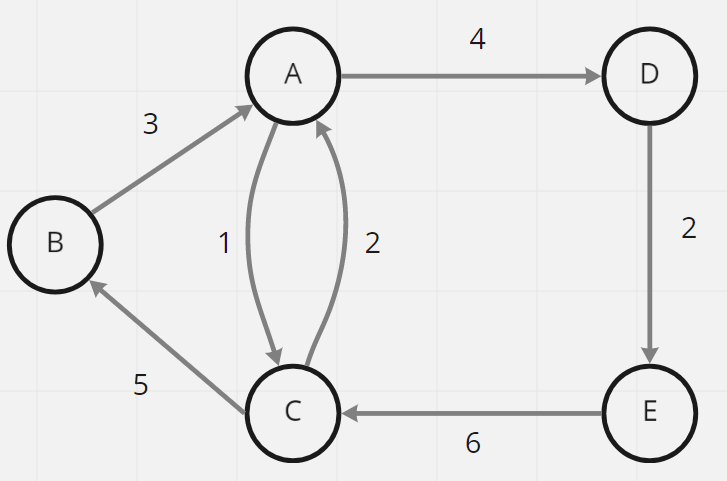
加權圖( Weighted Graph )

每條路線都有標記一個數字，稱為權重分數，這邊的權重分數可以是時間、成本、距離等等，加權圖最經典的應用就是處理最短路徑的問題，像是我要搭乘甚麼樣的交通工具才能最快到達目的地，Google map的交通工具規劃就是採用了這樣的概念。

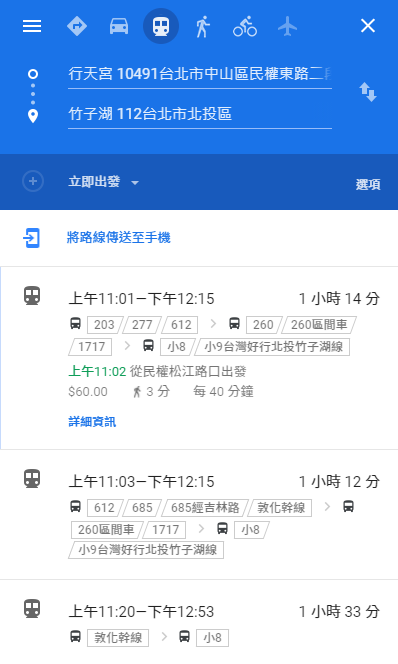
google map

Graph Traversal

如果想要走遍Graph裡面所有的節點可以有兩種做法，第一種方法是廣度優先搜尋 Breadth First Search(BFS)，我們可以先從一個故事來理解廣度優先搜尋的概念，有一天小王、 小李、小林他們三個人要結拜成三兄弟，因此辦了一個派對邀請所有朋友來共襄盛舉，在派對上「我」認識了一個很可愛的女生，只可惜當天沒要到連絡方式，也不知道對方的名字，只有一起拍了一張照片，回家後心心念念那個女孩，好想再見她一面，於是我決定動用我的人脈， 來找到那個心儀的女孩!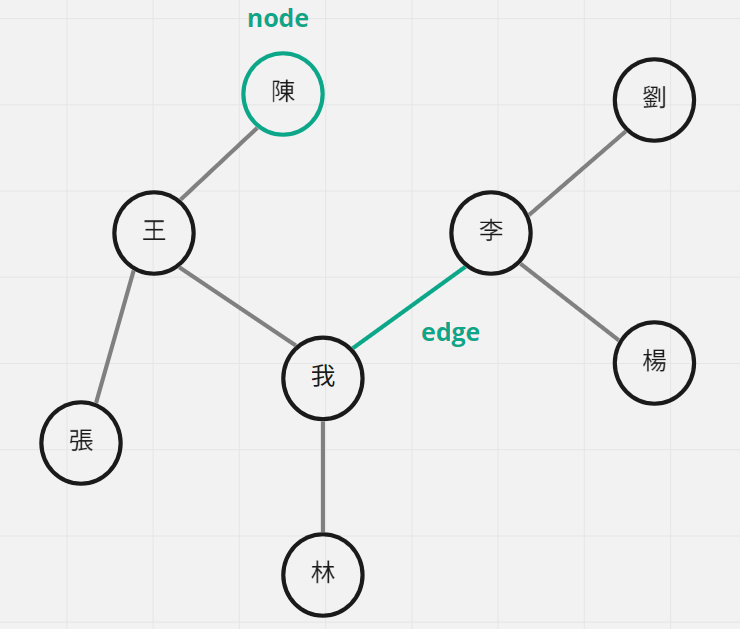

每個人都是一個節點(node)相鄰的節點會有邊(edge)連接著

於是我決定拜託我的三個好朋友，問他們認不認識這個女孩，結果三個朋友都說不認識，但很熱心地幫我問了他們的朋友有沒有人認識這個女孩，下圖的藍色節點代表是我認識的朋友，綠色節點則是朋友的朋友，所以我會先問過所有我認識的朋友(first degree第一層)，而我的朋友會再去問他們的朋友(second degree第二層)。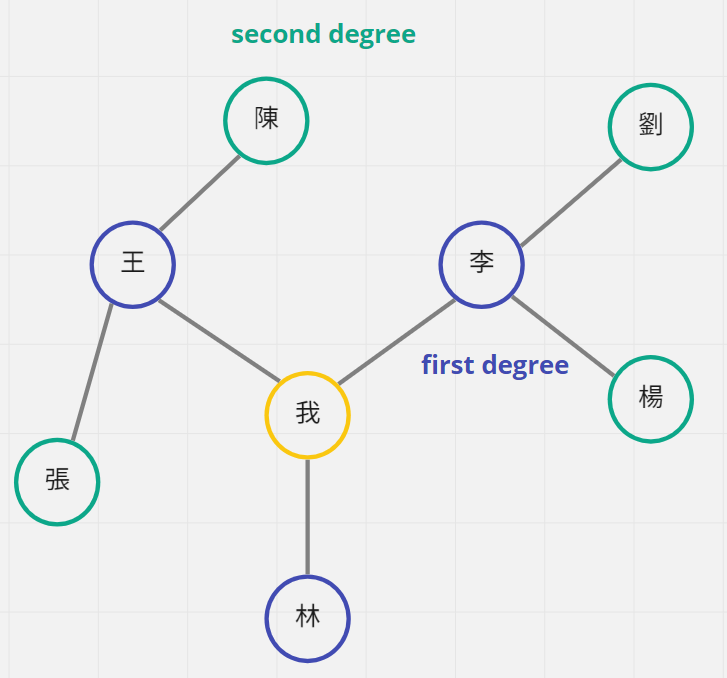

從上面的故事我們可以知道，廣度優先的搜尋順序會是先走訪相鄰節點，都走訪完了，就往下一層繼續走訪，廣度優先搜尋採用queue來實作，因為queue具有先進後出的特性，可以確保先搜尋到的節點，會優先成為下一個搜尋起點。
那麼就用js來實作Breadth First Search，在開始之前我們要先建立一個Graph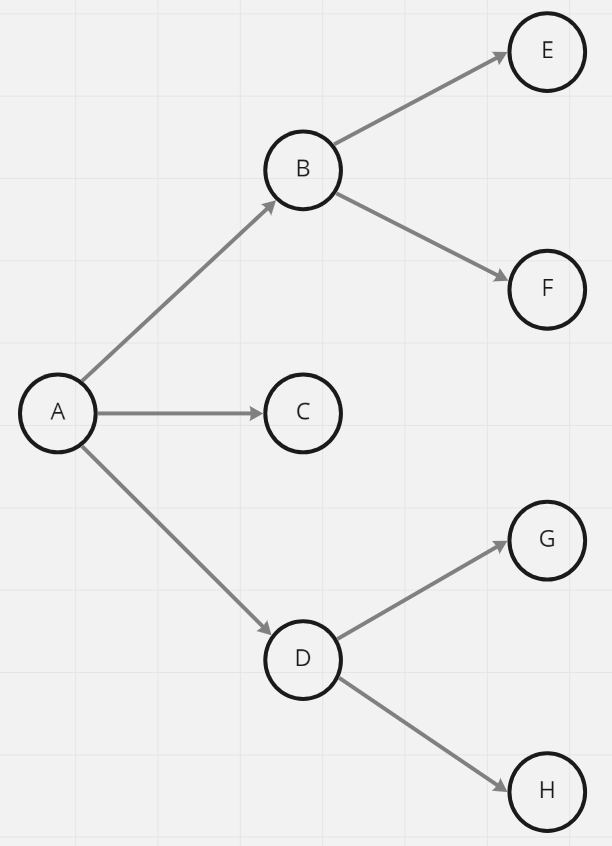

先用js實作出這個Graph

class Node {
    constructor(val) {
        this.value = val;
        this.neighbors = [];
        this.visited = false;
    }
    addNeighbor(n) {
        this.neighbors.push(n);
    }
}

let A = new Node("A");
let B = new Node("B");
let C = new Node("C");
let D = new Node("D");
let E = new Node("E");
let F = new Node("F");
let G = new Node("G");
let H = new Node("H");
A.addNeighbor(B);
A.addNeighbor(C);
A.addNeighbor(D);
B.addNeighbor(E);
B.addNeighbor(F);
D.addNeighbor(G);
D.addNeighbor(H);

用js實作Breadth First Search

const BFS = (starter) => {
    let queue = [];
    queue.push(starter);
    while (queue.length !== 0) {
        let firstNode = queue.shift();
        if (!firstNode.visited) {
            firstNode.visited = true;
            result.push(firstNode.value);
            firstNode.neighbors.forEach((element) => {
                if (!element.visited) {
                    queue.push(element);
                }
            });
        }
    }
    return result;
};

BFS(A);

//輸出結果 ["A", "B", "C", "D", "E", "F", "G", "H"]

把走訪過程圖像化的話會如下圖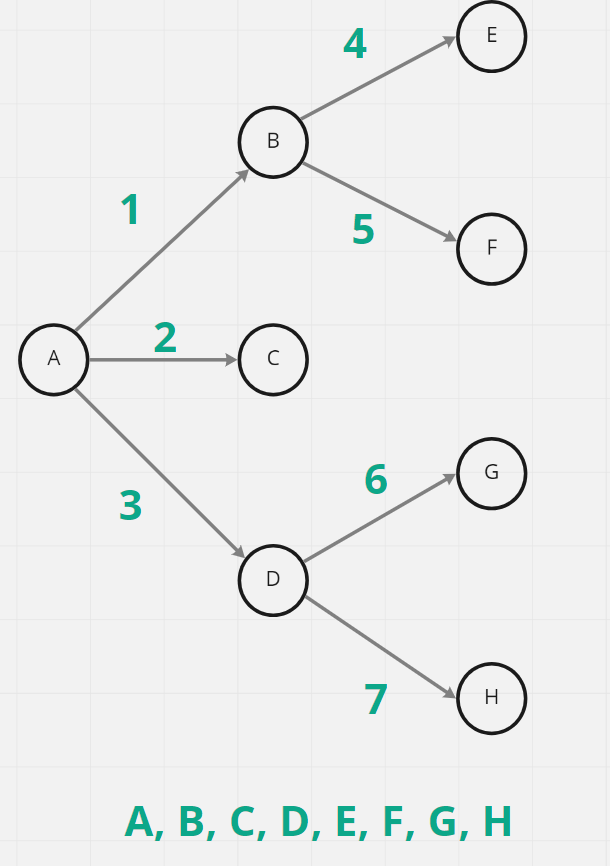

綠色數字為走訪順序

除了Breadth First Search之外，還有另一種搜尋方式叫深度優先搜尋 Depth First Search (DFS)，會先從一邊開始走訪，概念類似於走迷宮摸著牆走的概念，走到底了就折返，繼續往沒走過的節點探索，步驟如下:

• 從A出發，沿著上方的牆依序訪問，A, B ,E
• 走到E的時候發現是死路了，就折返到B
• 發現還有另外一條路再走到F
• 走到F發現又是死路，沿路折返到A
• 發現A還有其它相鄰節點，再走到C 
• 依序走下去…

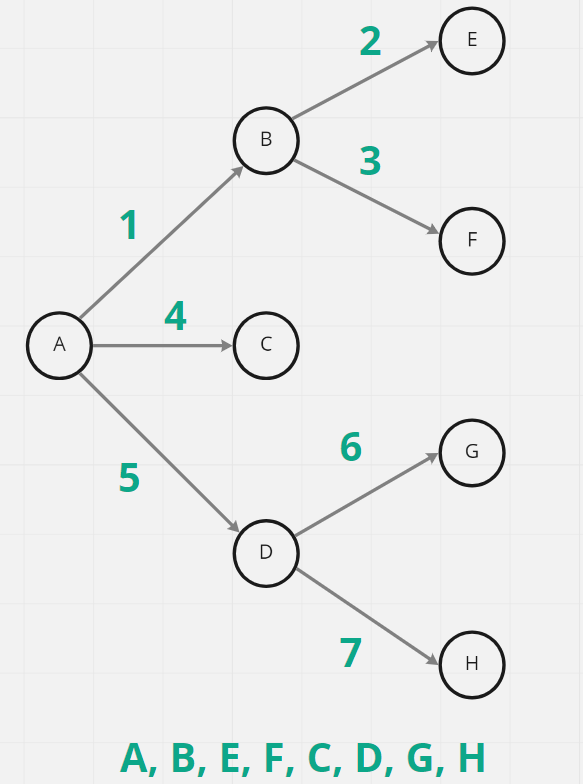
綠色數字為走訪順序

用js實作 Depth First Search

let result = [];
const DFT = (starter) => {
    starter.visited = true;
    result.push(starter.value);
    starter.neighbors.forEach((element) => {
        if (!element.visited) DFT(element);
    });
    return result;
};

DFT(A);

//輸出結果 ["A", "B", "E", "F", "C", "D", "G", "H"]

參考資料: breadth-first-search-a-simple-explanation