簡單來說就是函式自己呼叫自己的狀況，遞迴由兩部分組成

• Recursive Case(遞迴情況) - 當函式呼叫自己本身的情況
• Base Case(基本狀況) - 是當函式不再呼叫自己的條件，也就是終止的條件

遞迴提供了較為簡潔的寫法，不過一定要記得設定好終止的條件，避免進入無限循環，把記憶體吃光光。

階乘 Factorial

在學習遞迴的時候，大部分的人都會從階乘開始練習，因為大家高中數學都有學過階乘，來複習一下甚麼是階乘 ? 從1連續相乘到n為止，也就是n! = n*(n-1)* …21。

ex.5!=5*4*3*2*1

用js實作階乘

const factorial = (n) => {
    if (n === 1) return 1;
    return n * factorial(n - 1);
};

factorial(5);

遞迴在呼叫完自己後會先在原地等待，等待下一層將結果回傳，執行順序如下:

1. factorial(5)會等待 factorial(4)回傳結果
2. factorial(4)會等待 factorial(3)回傳結果
3. factorial(3)會等待 factorial(2)回傳結果
4. factorial(2)會等待 factorial(1)回傳結果

當n = 1的時候滿足終止遞迴的條件並回傳1

1. factorial(1)回傳1
2. factorial(2)回傳2*1 =2
3. factorial(3)回傳3*2=6
4. factorial(4)回傳4*6=24
5. factorial(5)回傳5*24 = 120

遞迴的執行過程可以參考下圖，紅色箭頭是呼叫函式，綠色箭頭是回傳結果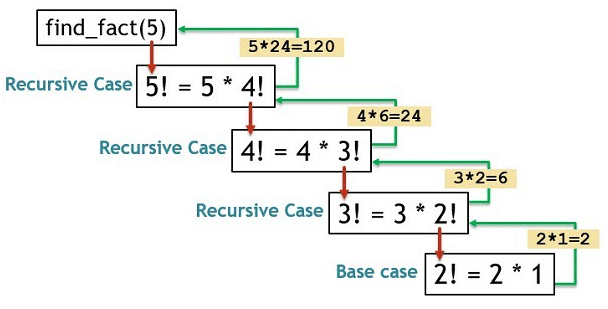

圖片來源:https://www.edureka.co/blog/recursion-in-python/

九九乘法表

以經典的九九乘法表為例，一般我們會直覺地用雙迴圈來寫，其實用遞迴也可以寫出九九乘法表。

//一般寫法
const print99 = () => {
    for (let i = 1; i <= 9; i++) {
        for (let j = 1; j <= 9; j++) {
            console.log(`${i}*${j}=${i * j}`);
        }
    }
};

print99();

//用遞迴(在前端群組看到hello大分享的寫法)
const print99ByRecursive = (i, j) => {
    console.log(`${i}*${j}=${i * j}`);
    if (j < 9) return print99(i, j + 1);
    if (i < 9) return print99(i + 1, 1);
};

print99ByRecursive(1, 1);

斐波那契數列

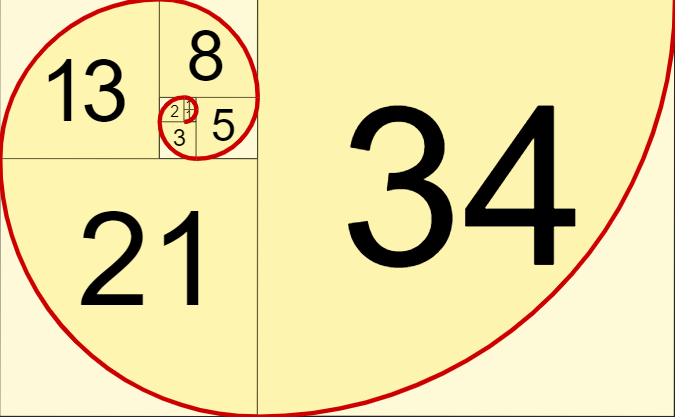
圖片來源:https://www.mathsisfun.com/numbers/fibonacci-sequence.html

經典的fibonacci sequence斐波那契數列就很適合用遞迴來解

甚麼是斐波那契數列?

斐波那契數列由0和1開始，之後的斐波那契數列就是由前兩位數字相加而得出 ，也就是第n項為第n-1和第n-2項的總和  - 引用自wikipedia

圖片來源:https://www.mathsisfun.com/numbers/fibonacci-sequence.htmlex.

ex.若要取得數列中的第11個數字的話公式為: 89 = 55+34 (n11 = n10 + n9)

用js實作斐波那契數列

const fibonacci = (i) => {
    if (i === 0 || i === 1) return i;
    return fibonacci(i - 1) + fibonacci(i - 2);
};

fibonacci(5);

單看程式碼應該會覺得很抽象，所以可以搭配下面這張圖來看，由於斐波那契數列的規則是每個數字都是前面兩個數相加的總和，畫成圖的話會發現結構很像binary tree。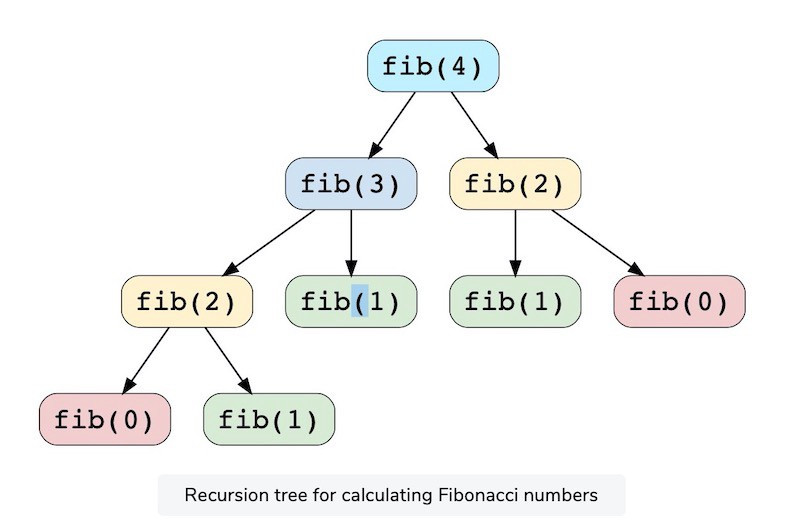

圖片來源:https://gopigorantala.com/fibonacci-number-java-ways-to-optimise-2/

不過眼尖的你可能會發現一個問題，有些函式明明已經有執行過，卻還是重複執行，像是fib(2) 、fib(1)，因為遞迴的本質是將問題拆解成多個小問題，而這些小問題可能會有重疊的狀況，因此並不會記得那些部分是已經運算過的，所以就會發生重複運算的問題，執行效率較差，這就是遞迴其中一個缺點。

除此之外，還可能發生stack overflow(堆疊溢位 - stack滿出來)的問題，在討論stack overflow之前，先來複習一下執行堆疊（call stack）的觀念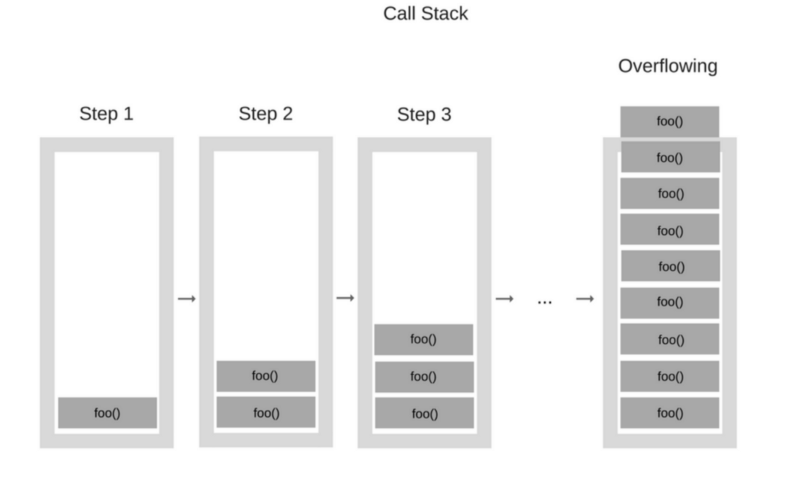

圖片來源:https://mlog.club/article/5741653

由於JavaScript是單執行緒的語言，一次只能做一件事情，所以使用具有後進先出特性的stack來儲存函式的執行環境，每次有新的任務加入的時候，就會像疊盤子一樣，一層一層往上疊加，JavaScript會先處理最頂端的函式，當函式執行完並且return之後，該函式就會被移除，接下來處理下一個函式，直到stack被清空為止。

因為遞迴會不斷的呼叫自己的特性，就會一直把函式添加到stack裡面，如果遞迴太深層的話就會發生stack overflow。

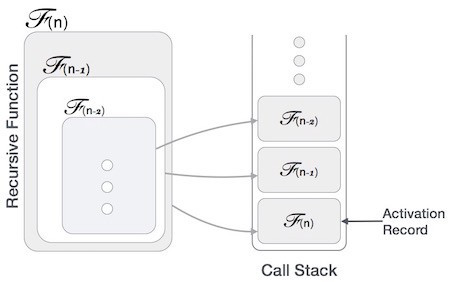
圖片引用:https://www.tutorialspoint.com/data_structures_algorithms/recursion_basics.htm

除了上述的問題，遞迴在呼叫函式的時候，為了保存當下執行的狀況，會將用到的區域變數、參數、返回位址暫存起來，因此會占用比較多的記憶體空間。

尾遞迴(tail recursion)

以往的作法會將運算結果儲存成區域變數，尾遞迴則是改將運算結果當成參數傳給下層的函式，這個情況稱為尾遞迴。

假設現在有個函式的功能是累加數字，用一般的遞迴寫法如下:

const recsum = (x) => {
    if (x === 1) {
        return x;
    } else {
        return x + recsum(x - 1);
    }
}

假如執行函式recsum(5)，則javaScript的執行順序如下，函式需要等待下一個函式，直到中止條件後才開始回傳結果，然後將值一個一個加總起來

recsum(5)
5 + recsum(4)
5 + (4 + recsum(3))
5 + (4 + (3 + recsum(2)))
5 + (4 + (3 + (2 + recsum(1))))
5 + (4 + (3 + (2 + 1)))
5 + (4 + (3 + 3))
5 + (4 + 6)
5 + 10
15

改成尾遞迴的話，變成使用傳入參數的方式來記錄當下累積的數字是多少

const tailrecsum = (x, running_total = 0) => {
    if (x === 0) {
        return running_total;
    } else {
        return tailrecsum(x - 1, running_total + x);
    }
}

執行的順序如下，可以發現初次呼叫的時候就開始計算累加值，不需要用額外的變數去紀錄，減少stack的用量

tailrecsum(5, 0)
tailrecsum(4, 5)
tailrecsum(3, 9)
tailrecsum(2, 12)
tailrecsum(1, 14)
tailrecsum(0, 15)
15

在查遞迴資料的時候一直看到這句話

遞迴只應天上有，凡人應當用迴圈

的確一開始接觸遞迴的時候，覺得有點超出大腦的負荷，因為遞迴不像迴圈那麼直觀好懂，直到看了大量的圖文解說，才比較理解遞迴的運作機制，其實遞迴能做的事，迴圈也可以做到，而且遞迴的執行時間還比較長甚至還比較佔用記憶體空間呢!但是遞迴的寫法通常會比迴圈來的更簡潔，可讀性更好，因此還是看使用的情境來評估要用遞迴或是迴圈來處理問題。

參考資料: 尾呼叫
what-is-tail-recursion