4 圖的走訪 - BFS 篇

如果要好好地探索一張圖，最經典的方法莫過於深度優先搜索(Depth First Search) 以及廣度優先搜索(Breadth First Search)了！深度優先搜索 DFS 是利用堆疊的概念，如果有發現一條道路通往尚未探索過的點，那麼就先把這個點的狀態暫時堆疊起來，先行探索下一個點，直到無路可進以後才回溯。廣度優先搜索 BFS 則是預先勘查好所有與目前這個點相連的所有點，將之標記後放入一個待處理的佇列，然後從這個佇列逐一重複相同的探索動作。

這兩種演算法有著非常非常多的應用，我們今天先來舉幾個簡單的例子。
（備註：我們今天討論的圖，都是無向、無權重的圖，是最單純的那類圖。）

4.1 尋找最短路線

想像一下我們有一些房間，而房間與房間之間有走廊連結著。

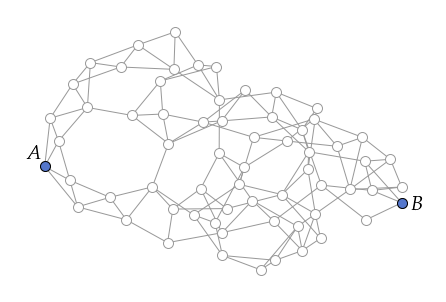
如果我們今天要從點A走到點B，這時候就可以從 A 開始利用廣度優先搜索，逐步探查 A 走一步可以到的點、然後到走兩步可以到的點、等等依此類推。如果我們將「探查誰從而發現誰」這樣的關係描繪出來，不難發現這樣會形成一個樹狀結構（我們通常稱它為 BFS 搜索樹）

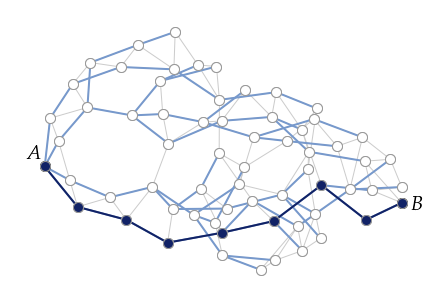
不是重點的參考程式碼(Python)：

from queue import Queue
import networkx as nx

def get_bfs_tree(G, start_node):
    """回傳從 start_node 開始搜索的 BFS 搜索樹、以及每個點的父節點。"""
    prev = dict()                 # prev 紀錄每個點是誰走過來的。
    prev[start_node] = start_node # 做個標記，表示走過了。
    q = Queue()
    q.put(start_node)
    H = nx.Graph()
    while not q.empty():
        u = q.get()
        for v in G.neighbors(u):
            if v not in prev:
                H.add_edge(u, v)
                prev[v] = u
                q.put(v)
    return H, prev

4.2 保持雙頂點連通分量的子圖

接下來跟大家分享一個把 BFS 演算法反過來應用在圖論中的有趣例子。
想像一下，如果這張圖 G 代表一個網路。每一條邊都代表連接兩個節點的某條網路線，我們想要找出這個圖的子圖 H（也就是保留某些網路線），使得任兩點之間仍然可以進行資料傳輸（可以是直接或間接的資料傳輸）。顯然隨便找一棵生成樹就可以了，如果我們想要額外增加條件：如果某個節點壞掉了，在原本的圖 G 上面仍然連通，在這個子圖 H 上也必須要連通。

在這樣的條件之下，我們說這個子圖 H 是保有圖 G 的雙連通分量特性的！要怎麼實作呢？想必各位也已經猜到了，沒錯就是使用 BFS！如果我們對這張圖 G 做兩次 BFS（第二次的時候可能有些地方會斷開，就對每個連通分量各自做一次 BFS 就行了），這些蒐集起來的邊，可以經過神奇的數學證明，它滿足我們想要的保持雙頂點連通分量的條件！

4.X 冷笑話

為什麼把一張圖燒掉以後，時間很快就過了呢？因為，這一切都太圖燃了啊...