3 圖的資料結構

今天來介紹我們儲存一張圖的時候，幾種常見的資料結構：相鄰矩陣(Adjacency Matrix)、鄰接鏈結串列(Adjacency Linked List)、邊列表(Edge List)。

3.1 相鄰矩陣 Adjacency Matrix

意思就是一個二維陣列啦，其中 (i, j) 格子裡面放的是「到底有沒有一條從 i 到 j 的邊」之類的訊息。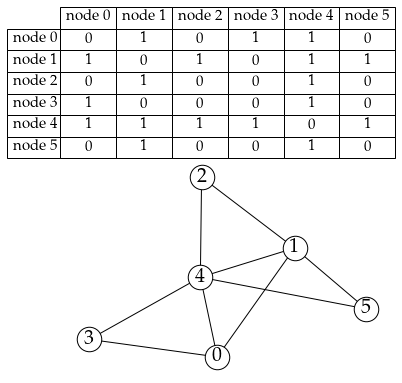

3.2 鄰接鏈結串列 Adjacency Linked List

簡單來說就是用鏈結串列記錄下所有一個點的鄰居。

嗯...用 networkx 畫 linked list 感覺還是太勉強了哈，上面那張相鄰矩陣畫了好久...

3.3 邊列表 Edge List

如果一條邊很重的話，就讓他們保持在輸入時候的樣子，此外我們再用一些指標來表示「這個點的下一條相鄰邊在哪裡」之類的訊息，就可以有效率的存取囉。

3.4 選擇障礙

大家可以先想看看這個問題：如果我要修改這個圖怎麼辦？如果我想要支援 "增加一條邊" 和 "刪除一條邊" 的操作，使用哪種資料結構比較好？

一個粗淺的答案是：這取決於圖的種類與不同操作的頻率。考慮一個無向圖，那麼當你增加一條邊的時候，相較於邊列表而言，可能要處理 A[i][j] 和 A[j][i]，這可能牽涉到兩次分頁錯誤(page fault)。當你刪除一條邊的時候，如果使用相連鏈結串列，相較於相鄰矩陣來說，可能得花更多時間找到那條要刪除的邊。

完美的資料結構並不存ㄗ
(這句話好像不是這樣用的)

籠統地說，資料結構就是在電腦中儲存資料的形式。但其背後蘊含的意思，則是結合了類似 API 和封裝(encapsulation)的效果(可參考維基百科)。根據不同的使用需求，而修改或設計出相對應的資料結構，才會讓演算法變得更有效率。

3.5 根據需求變更設計

如果我們所要解決的圖論問題，其輸入都有一定的特徵，那麼我們可以特化資料結構，並能實作出更有效率的演算法。列舉一個簡單的例子，通常我們使用鄰接鏈結串列，是因為我們無法保證每一個點的度數(degree)有多少。然而，如果對於程式的運行有所理解的話，會知道存取鏈結串列這件事情，會讓程式需要在記憶體中零散地存取多處，從而造成很多的快取失誤，進而拖累程式的執行效率（雖然說現在大家都用 vector 了就是...）

假設現在我們考慮的圖，是固定度數的（這類圖我們稱之為正則圖 regular graphs），那麼我們在設計資料結構的時候，只需要預先幫每個節點開設好固定大小的空間，便能更有效率地存取這些鄰接表格。

如果輸入的圖並沒有一定的規則，但說不定能事先將之轉換為固定規則的圖，再存起來，也可以達到類似的效果。舉一個例子來說，如果我們不確定一棵樹裡面，每個節點的孩子數量為何，我們可以把這棵樹以左子右兄弟(left-child right-sibling)的方式，轉換為一棵二元樹，這樣每個點的度數就不超過 3，此時也就能夠用一個簡單的 struct 就能描述一個節點了。

3.X 冷笑話

完全圖和稀疏圖誰的節點看久了會近視呢？答案是完全圖，因為它們都是高度數。