試題反映理論

在試題反映理論(Item Response Theory, IRT)中
能用作因素來解釋答題表現的稱為「能力」
而答題的表現以機率呈現，範圍為區間[0,1]
其中，0 : 必錯；1 : 必對

每一個試題(Item)都應當有一個自己的特徵曲線
其 x軸表示能力， y軸表示答題表現
且此特徵曲線所對應之函數應為遞增函數
表示根據所應對的能力越大，則答題表現越佳(越有機會答對)
該曲線稱為「試題特徵曲線(Item Characteristic Curve, ICC)」

(圖片來源：試題反應理論的介紹---余民寧)
下圖為一些ICC的介紹，詳細內容可參考文獻
這些圖中，我主要關注在圖d,e,f上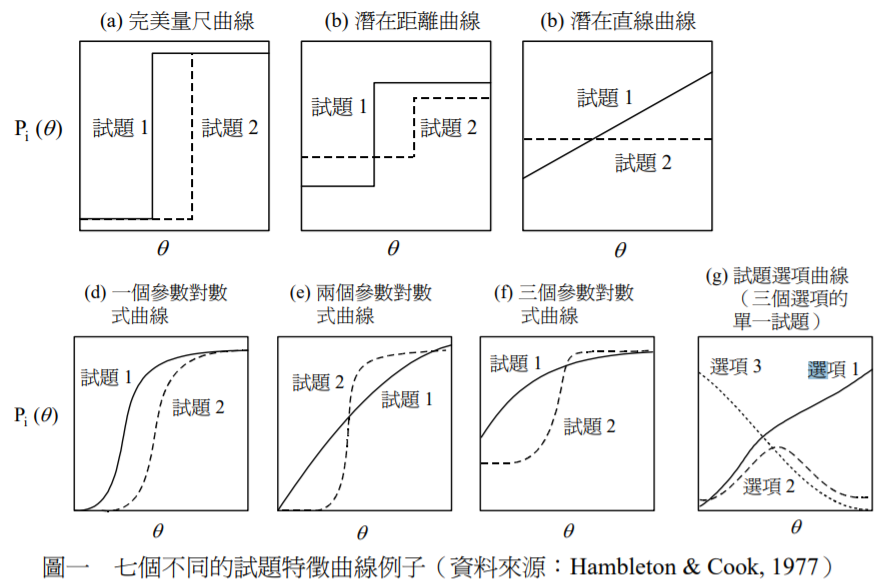

三參數對數模型(3PL)

在三參數對數模型中
是考慮了「鑑別度(a)」、「答對率(b)」、「猜測度(c)」為參數的模型
其中 D 為 1.7 (我也不知道為什麼@@)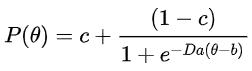

依次說說為什麼a, b, c的位置在那裏

1. b:答對率(難度)
   我們希望這個參數可以表達出作答者的程度與該題難度的差異能影響到答題表現
   故會有 此項
   當猜對度為0且 時，其答對率為0.5

2. a:區分度
   「區分度」想表達的是「是否存在一個臨界值，使得小於該值的人的答對率 << 大於該值的人的答對率」
   如果考慮此參數，他會表現在ICC的最大斜率上(通常在 時)
   也就是該點的前後答對率差異最明顯
   故區分度越高，此段越陡；區分度越低，此段越平緩

3. c:猜測度
   有些題目即使完全不會做也能靠猜的答對(選擇題)
   故考慮猜測度就是要把這種可能性考慮進去

但是IRT的各參數很難去做估計值
因為我看了許多篇文章
看起來不是單純的用「答對率」、「鑑別度」估計「難度」、「區分度」
故在這之後我主要是取其ICC圖形做改動

參考文獻：
試題反應理論的介紹---余民寧