yo, what's up

本章要來介紹 FP 的重要觀念，Algebraic structure!

What's Algebraic structure?

In mathematics, and more specifically in abstract algebra, an algebraic structure on a set A (called carrier set or underlying set) is a collection of finitary operations on A ; the set A with this structure is also called an algebra. - James Sinclair

而簡單來說，可以把它想像成一組元素的集合(又稱 Object)，其包含一些操作(operation)在裡面，而這種結構又稱 Algebra.

註: 這裡的 Object 並不是 JS 的 Object，可以先把它想像成一個 Container 裡面封裝的一些元素.

像是 Semigroup, Functor, Applicative 跟 Monad 這些陌生的名詞，其實都是基於此一概念，它們都屬於 Algebraic structure.

而未來也會介紹一系列的 Monad 像是處理 Side Effect 的 IO Monad, 處理錯誤情境的 Either Monad 等等，其背後都有相同的 method 名稱，像是 .map, .ap, 又或是 .chain。 這並不是巧合，每個 method 背後都遵循同典範 (pattern)，沒錯，就是 Algebraic structure.

Algebraic structure in JavaScript

當初讀者在研究 FP 的時候，曾經懷疑會想為何一定要遵循同典範，內心就想為何不能(又或是沒有套件開發者)把 method 像是 map， 將它的名稱改成 then 之類的，為何不能有屬於自己的 style!!!!

以 JavaScript 為例，其實有一個讓開發者參照的規格書，就是 fantasy-land spec，內容並沒有告訴套件開發者該如何實作，只有列出規範，例如 method 的名稱，以及它該符合哪些特性(law)。

下面就是 fantasy-land 對於列出 Algebraic structure 的關聯圖，並對其進行規範，並且套件開發者等就會有共識地去遵從這些規範。

Example

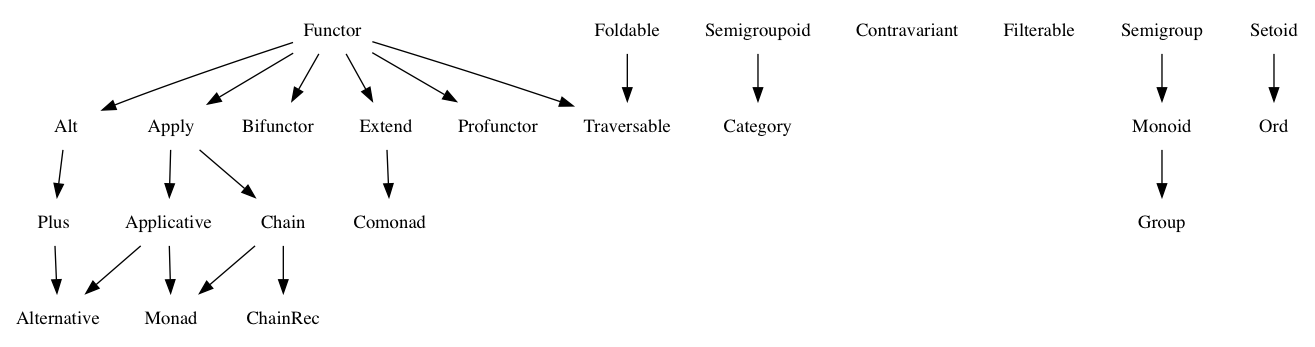
舉例 Setoid 這個 Algebraic structure 為例，在 fantasy-land spec 中，其規範了 method 跟 其必須遵循某些特性

method (HM Type signature)

順帶一提，前一篇提到的 Setoid 在 fantasyland spec 並不是

equals :: Setoid => a -> a -> Boolean

而多了新的符號 ~> 在內

equals :: Setoid a => a ~> a -> Boolean

~> 的意思就是 a 必須要有 equal 這個 method，而 ~> 右方才為 equal 的 signature.

整句就是若 a 是 Setoid 且有 equals 這個 method 在內， 則 a -> a -> Boolean 成立。

law

並且如果 a 為 Setoid 必須符合哪些三項特性(law)

1. reflexivity:

a.equals(a) === true

2. symmetry

a.equals(b) === b.equals(a)

3. transitivity

a.equals(b) && b.equals(c) === a.equals(c)

implement

現在來實作出一個比較是否為兩值是否相等的 Setoid 吧!!

import * as R from 'ramda';

const Setoid = (val) => ({
    val, 
    equals: o => R.equals(val, o.val),
    inspect: () => `Setoid(${val})`
})

Setoid('Functional Progamming').equals(Setoid('Functional Progamming')) // true

Setoid('Functional Progamming').equals(Setoid('Object Oriented Progamming')) // false

而這裡使用 ramda 所提供的函式 equals， 雖然簡單，但這是我們實作的第一個 Algebraic structure!

讀者們可以驗證一下是否符合 fantasy-land 的規範!

小結

富間了，富間了，決定將 Type class 跟 ADT 的概念一到下一章，這章就先簡單介紹 Algebraic structure 相關概念!

而 TS 對於其定義更嚴謹(理論上是更貼近真正的概念)，此次範例只是簡單 demo Algebraic structure 的概念，範例僅作教學用途，不適合用在 Production 上。可以使用 fp-ts 的 Setoid。

歡迎來到 Functional Programming 的世界!

Reference

1. fp-ts equals
2. Algebraic structure