今天的題目是要我們在一個整數陣列中找到子陣列（subarray），也就是擷取陣列中相連的一部分，求出擁有最大的總和並且回傳

而會讓題目變得複雜的原因，是因為我們必須要考慮陣列中有包含負數。
如果是正整數陣列一定是整個加起來對吧？
假設今天我們有一個陣列為 [3, -2, 4]，
我們可以得到 3+ (-2) + 4 = 5 獲得的總和比我們只拿３或４都還多，
但如果今天拿到的是[3, -5, 4]這時候我們就要單拿4會比較好。
因為-5後面的４不足以彌補-5對我們的傷害。

所以我們需要判斷的應該就是：
負數後面出現的數到底有沒有足以抵過他對我們的重擊再決定要不要涵蓋這個數對吧？

不過，光按照這個想法去解，我們還是很難想到要怎麼去實作。
這時候 Kadane's algorithm就派上用場了！
推薦閱讀：Kadane’s Algorithm — (Dynamic Programming) — How and Why does it Work?
這一題要使用Dynamic programming來解，還記得DP的觀念嗎？
我們在Day03有提過，忘記了可以複習一下！

我們將從頭開始去記錄我們取到Array哪裏(也就是index)，
每一次我們都會取目前可以得到的最大值，記錄在目前的index。

也就是我們可以決定取前面那個數目前的總和加上當下的數，
或是放棄前面的總和，歸零從現在當下的數開始累加。
MaxSumHere = max( MaxSumHere + 當下的number, 當下的number)

我們以這個原則，開始對陣列做檢查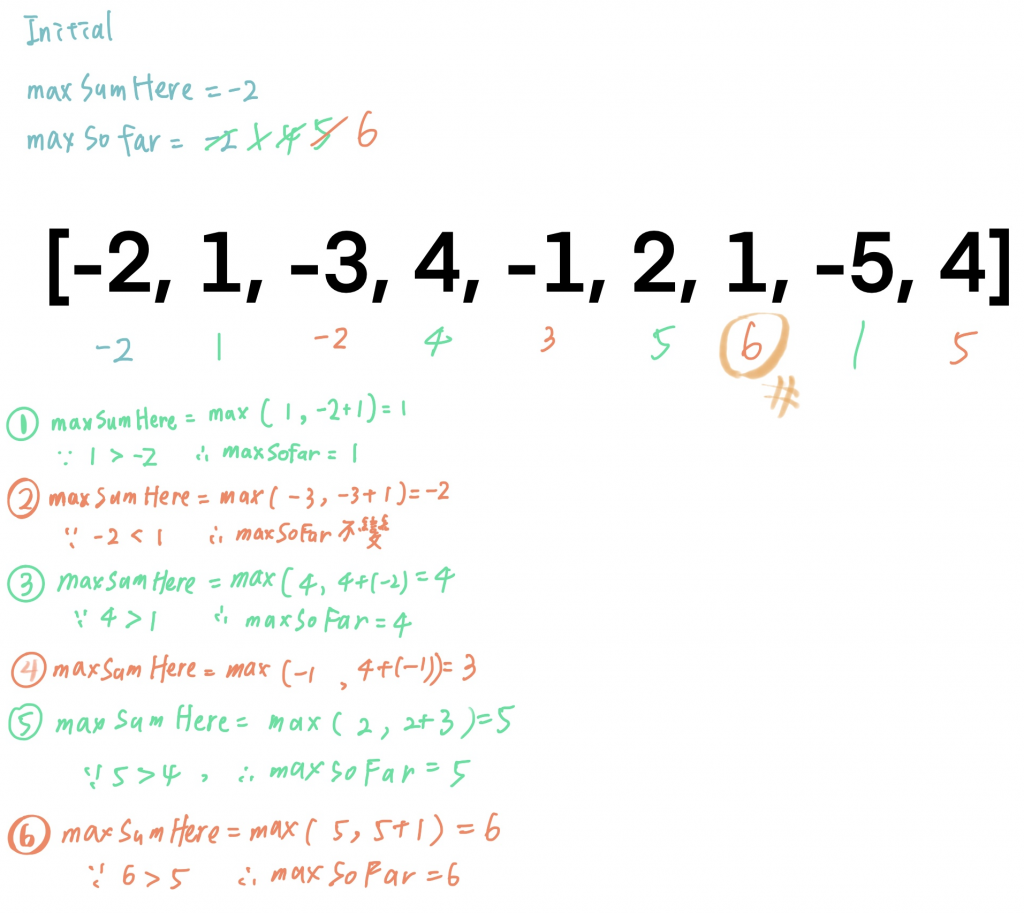

以上圖為例:
一開始 MaxSumHere = -2
第一步驟我們比較現在的數 1 和 -2 + 1 = -1 取大的，也就是 1
代表我們目前的總和是１，又因為 1 > -2 所以目前的最大值會是１

第二步驟：比較 -3 和 -3 + 前面目前的最大和 1， 也就是 -2
但因為 -2 < 1，所以我們的目前最大總和不變

我們不段重複這個規則，直到這個陣列被拜訪結束。
最後找到我們紀錄中最大的數，就是題目要的答案。

Kadane's algorithm 很棒的地方在於：
我們不用一直重新循環檢查，我們只需要拜訪陣列一次，並且用一個變數來暫存我們目前存的最大總和即可。

此外，題目沒有要我們回傳一整個subarray，只是要最大的結果，所以我們只需要做在每一步驟時，另外比較當下的結果有沒有比目前暫存的最大值還大，若有則取代，我們就不需要最後才去找出最大值。
時間複雜度為 O(N)，空間複雜度為 O(1)

最後來看實作吧!

var maxSubArray = function(nums) {
    let maxSumHere = nums[0];
	let maxSorFar = nums[0];
	for (let i = 1; i< nums.length; i++){
		const num = nums[i];
		maxSumHere = Math.max(num, maxSumHere + num);
		maxSorFar =  Math.max(maxSorFar, maxSumHere);
	}
	return maxSorFar;
};

明日題目預告：
凱撒密碼的運用：Shifting Letters