看完這題題目
還記得小時候很常被問到：
給你一些數字，請你從這些數中用最少的數，來涵蓋最多的範圍。於是我們就會拿起筆開畫數線。不過今天，我們要用程式碼來解題，沒有了畫筆，我們該如何下手？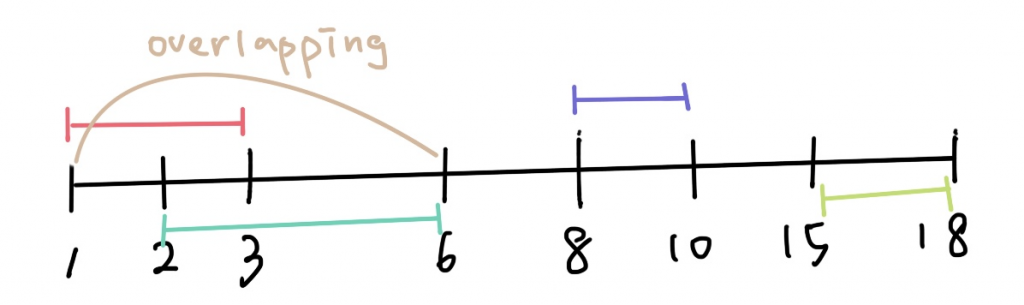

Input: intervals = [[1,3],[2,6],[8,10],[15,18]]

在解題之前我們先想想要如何在陣列中長得像這樣[starti, endi]的元素。只依靠start和end，來決定是否有區間重疊，畢竟我們從畫圖很容易可以看得出來哪些元素共享哪幾個重疊的數，但如果現在我只告訴你頭尾兩個數，我們是不是需要去比較區間才能知道？

這裡我們隨意抓出第一和第二個元素也就是[1,3]和[2,6]
我們可以推斷：如果第一個元素的 end ≥ 第二個元素的start （3 ≥ 2），就代表有重疊發生

但如果今天的範例長成 intervals = [[8,10],[2,6],[1,3],[15,18]]
我們一樣抓出第一和第二個元素也就是 [8,10],[2,6]

依照前面的推斷，因為 10 ≥ 6，所以有重疊！？ 完蛋！

也就是說，我們先前可以輕鬆地抓兩個元素來比較是因為：前面的範例恰好每個元素的start是由小到大排列的，也就是說我們應該要確保，每個元素的排列是依照前面的元素大小來排列。

接著再思考一個問題，我們要如何合併多個有重疊的元素，像是我們在原本的範例再多塞一個變成

intervals = [[1,3],[2,6],[5,7],[8,10],[15,18]]
我們應該要把 [1,3],[2,6],[5,7] 合併成 [1,7]

我們可以先把[1,3] 和 [2,6]合併成 [1,6]後，再用[1,6]和[5,7]下去做合併變成[1,7]。
但我們要如何產出[[1,7],[8,10],[15,18]]這個答案？
我們是不是在過程中有一個[1,6]消失了？

也就是說假設我們有一個暫存區空陣列[]，我們把[[1,6]]加入後，往下走到[5,7]，我們應該要拿[5,7]去和暫存區內的[1,6]確認，看看他們有沒有需要合併，如果下個元素的start≤前一個暫存區的end，就代表有合併的動作要做。
我們取暫存區的end(6)和下個元素的end(7)，｀取大的當作end｀，直接可以把暫存區這個元素的end替換掉，產生了[1,7]！

那為什麼我們要取大的元素當end，而不直接取後面的？
因為有可能會有[[1,7],[3,6]]這種被涵蓋的情況發生。

總結我們要做的事

1. 把元素按照start排序
2. 建立一個空[]放output
3. 一開始直接把第一個元素塞到output
4. 相鄰的元素利用是否 前面元素的 end ≥ 後面元素的start，如果有則要做合併，改變end的操作

以上的做法，時間複雜度為Ｏ(nlogn)→主要花在排序，空間複雜度O(n) → 我們的ouput，因為最糟為都沒有重疊

最後就是實作程式碼。
希望看完上面的解釋，希望你也覺得這題根本就跟畫數線一樣簡單拉！

var merge = function (intervals) {
  const sortIntervals = intervals.sort((a, b) => a[0] - b[0]);

  const output = [];
  let current = sortIntervals[0];
  output.push(current);

  for (const next of sortIntervals) {
    const [currentStart, currentEnd] = current;
    const [nextStart, nextEnd] = next;

    if (currentEnd >= nextStart) current[1] = Math.max(currentEnd, nextEnd);
    else {
      current = next;
      output.push(current);
    }
  }
  return output;
};

明日題目預告：Maximum Subarray