今日題目

題目連結：108. Convert Sorted Array to Binary Search Tree
題目主題：Array, Divide and Conquer, Tree, Binary Search Tree, Binary Tree

今天的會開始進入 Binary Search Tree 的主題，這次題目是滿重要的觀念題，需要先瞭解 Binary Search Tree 的基本原則。

簡單說說 Binary Search Tree

Binary Search Tree 是一顆有原則的樹，原則如下：

1. 越小的數字在越左邊的節點
2. 越大的數字在越右邊的節點
3. 左邊子節點一定小於父節點的值
4. 右邊子節點一定大於父節點的值
5. 通常不會有節點出現重複的值

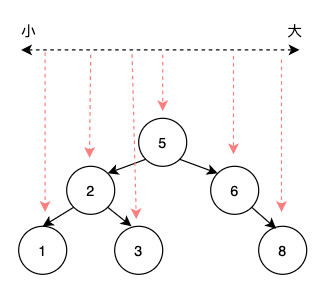
可以看看上圖的範例，是一個符合Binary Search Tree 原則的樹。

題目解說

建議可以看看LeetCode原本的題目說明，這邊是用我的方式說明題目，參考就好。

題目會給一個 nums 陣列，這個 nums 裡面的值已經將順序從小到大排好，本題的目標是將這個 nums 轉成一顆 Binary Search Tree。另外這個 Binary Search Tree 要是一顆高度平衡的樹，左邊節點與右邊節點深度不會超過一個。

約束：

• 1 <= nums.length <= 10的4次方
• -10的4次方 <= nums[i] <= 10的4次方
• nums 裡面的值會從小到大排好

範例1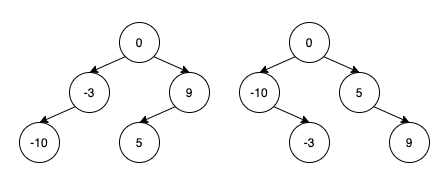

輸入: nums = [-10,-3,0,5,9]
輸出: [0,-3,9,-10,null,5]
解說: [0,-10,5,null,-3,null,9] 也是可以接受的答案，如上圖所示，兩種答案都可以是高平衡的Binary Search Tree。

範例2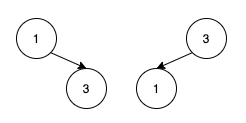

輸入: nums = [1,3]
輸出: [3,1]
解說: [1,3]也是可以接受的答案，如上圖所示，兩種答案都可以是高平衡的 Binary Search Tree。

建議到這邊先停下來，嘗試自己解解看，若沒有想法可再繼續走下去。

解題的想像

此題目的解法，可以先有這樣的想像，基本上一個排序好的陣列，要轉成 Binary Search Tree 的感覺如下圖:

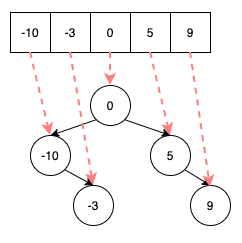
可以看到其實概念就是把中間的值當根節點，左邊跟右邊在分別一個一個拉下來就可以形成一個高平衡的Binary Search Tree，下面的圖解過程會有更清楚的圖片說明。

文字描述

1. 寫一個遞迴方法，傳入要轉Binary Search Tree的陣列、開始位置、結束位置、目前節點，最終回傳完整的一顆TreeNode組成的樹。
2. 此方法第一次呼叫會找到根節點，因為是高度平衡的Binary Search Tree，會用開始位置及結束位置找出中間的位置當根節點，公式為 (startIndex + endIndex) / 2。
3. 找到中間位置 nums[middleIndex] 就會當作目前的節點。
4. 第二次以後呼叫方法，會開始分別傳入目前節點的左邊節點及右邊節點，用一樣的方法找到節點的值，會一直遞迴到 nums 每個值都轉到這棵樹裡面。

圖解過程

範例：nums = [-15, -10, -3, 0, 5, 9, 13]

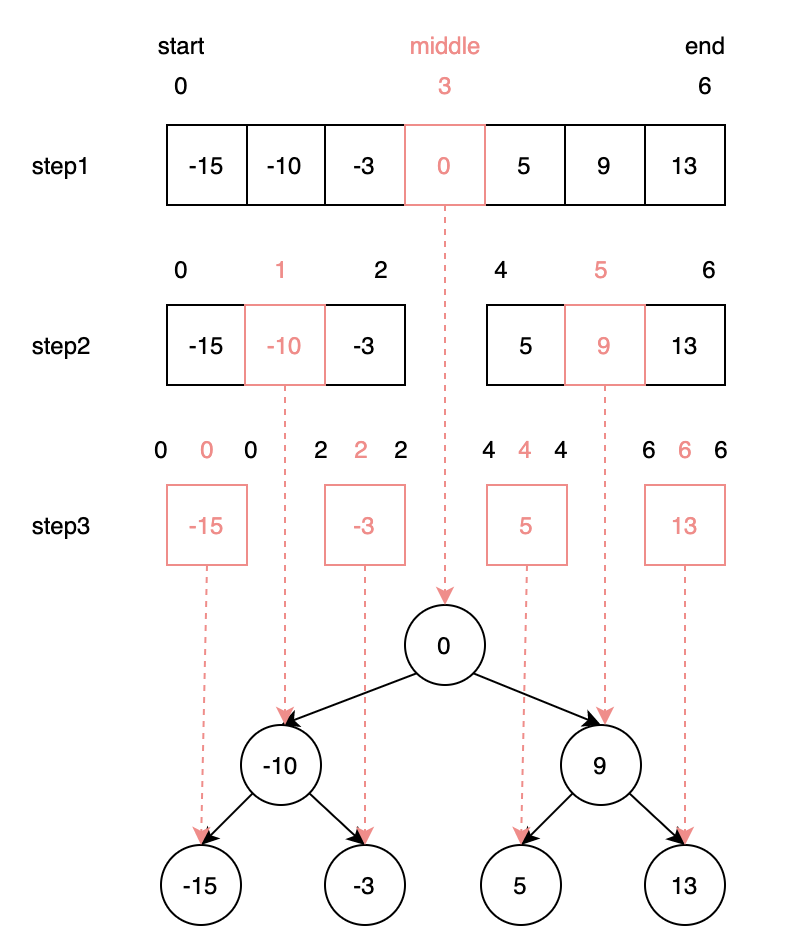
上圖中，可以從 step1 開始看，每一回合我們都會有一個開始跟結束的位置，每次都會找到一個middle位置，而 step1 找到的就是我們的根節點。

step2 會在把 step1 的middle位置左邊跟右邊都分割下去，走一樣的步驟，在分別在用開始跟結束位置找出middle位置，就會是根節點的兩個子節點。

step3 再從 step2 分割下來，因為已經剩一個值了，因此開頭結束及中間都會是同一個位置。最終形成下面的高平衡 Binary Search Tree。

這次的圖解過程跟實際程式跑起來的順序可能會有些差別，實際程式運作過程會比較類似Preorder的方式在找節點的值，會從左邊的節點開始走完才會開始找右邊的節點的值，只是在想像的過程個人覺得用上圖的方式想像會比較順。

若因為沒想法而走到這邊，建議看完想像以後再給自己一次機會試一次。

程式碼撰寫

class Solution:
    def arrayToBST(self, nums, startIndex, endIndex, node:TreeNode = None):
        # 開始位置若大於結束位置，代表沒有節點了
        if startIndex > endIndex:
            return node
        # 找到中間節點當目前節點
        middleIndex = int((startIndex + endIndex)/2)
        node = TreeNode(nums[middleIndex])
        # 找到目前節點的左子節點
        node.left = self.arrayToBST(nums, startIndex, middleIndex-1, node.left)
        # 找到目前節點的右子節點
        node.right = self.arrayToBST(nums, middleIndex+1, endIndex, node.right)
        
        return node
        
    
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        return self.arrayToBST(nums, 0, len(nums)-1)

希望您今天能瞭解到...

1. Binary Search Tree 的基本觀念
2. 108. Convert Sorted Array to Binary Search Tree 的解題方法

若內容有什麼問題或建議歡迎一起交流：）
感謝您今天願意花時間看完這篇文章~~~~

Next：700. Search in a Binary Search Tree