●There may exist various algorithms for the same problem.
●We then compare these algorithms by measuring their efficiency.
●To do so, we estimate the growth rate of running time in function of input size n.
●We proceed to introduce the notion of time complexity.
●Similar to time complexity(時間複雜度), we later turn to the notion of space complexity(空間複雜度).
EX:Sum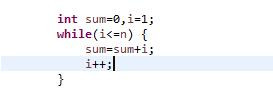

第一行時間加總是2
第二行時間加總是n+1
第三行時間加總是2n
第四行時間加總是n
總共是4n+3
Big-O Notation
Big-o定義: f (n) ∈ O(g(n)) as n →∞
若有一個常數 c > 0 還有一些n0,那麼 f (n) ≤ c ×g(n) ∀n ≥ n0.
快速判斷時間複雜度的方法:
1.Keep the leading term only.留著首項
2.Drop the coefficient.首項常數拿掉
3. time complexity.即為時間複雜度
EX:1. 8n^2 −3n + 4. ∈ O(n^2) 2.4n+3∈ O(n)
有一個k層迴圈的規則,當有一個k層迴圈則時間複雜度為O(n^k)。