「不是那個MAC。 不對，也不是漢堡。」

MAC能吃嗎？

先前我們介紹了數位簽章，今天我們要介紹的是MAC（message authentication code）訊息鑑別碼。

訊息識別碼同時擁有數位簽章和雜湊函數的性質。
他可以驗證訊息的完整性、可以任意輸入固定輸出長度、可以確認來源。
但是他沒有不可否認性，而這個是數位簽章有的。

然後當然，不能吃。

我們來講一下MAC的操作。

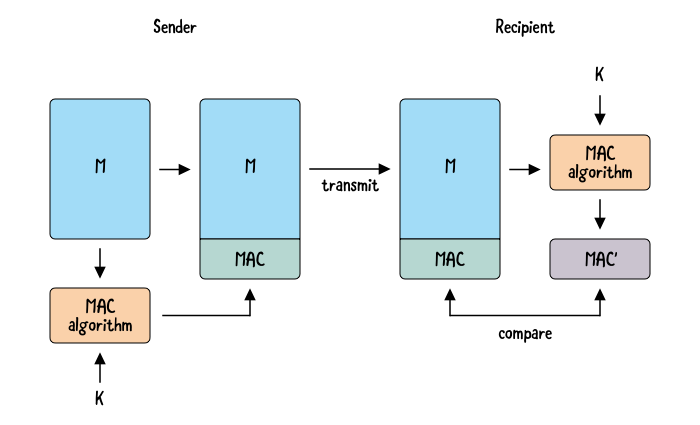
傳送者將訊息用密鑰 k 經過MAC運算之後加在訊息本身之後，並整批傳送給對方。
密鑰 k 也要用安全的通道傳送。
收件者將收到的訊息中，原訊息的部分，用密鑰 k 進入MAC運算，運算結果和傳過來的訊息比對。
如果相同就證明訊息是完整的。

可以看到，MAC是一種對稱式加密，傳送者和接收者必須擁有同一把密鑰。
既然雙方擁有同一把鑰匙，就沒有辦法證明訊息是由誰所生成。
也就是說沒有不可否認性。
白話一點來說，Alice 可以說這個訊息不是他傳的，因為 Bob 也有同一把鑰匙。

所以 MAC 好在哪？

快。

還記得我們說過對稱式加密比非對稱式加密還要快嗎？
MAC 是一種對稱式加密（我們等一下會說怎麼算），
而數位簽章是公鑰加密，
理所當然的，MAC 會比數位簽章快。

HMAC

聽起來超猛的，有一種 X-men 的感覺，超級英雄，wow。
扯遠了。

HMAC 的 H 就是 HASH（雜湊函數） 的意思。
我們利用 HASH 來達到訊息識別碼的功能。

首先密鑰要經過填充成為擴充密鑰。
如上圖，這個擴充密鑰要和 IPAD 和 OPAD 做 xor 。

其中IPAD （inner pad）跟 OPAD（outer pad） 是兩個常數。

和 IPAD xor 後的 k 接在訊息的後面進入雜湊函數運算，
運算結果接在「與 OPAD xor 後的 k」之後，進入雜湊運算。
運算結果即是輸出值。

CBC-MAC

如果你對這串東西沒有印象的話，請回去複習區塊密碼的操作模式。
他排在第一位，區塊鏈的那位。

當時挖了一個坑，說 CBC 還有一個功能是訊息鑑別碼。
過了十天，我們就來看這是怎麼回事。

CBC 就是區塊鏈的意思（直翻的話），也就是前一個區塊加密結果會影響下一個區塊的加密結果，
我們之前說的 CBC 會把每一輪的加密結果儲存下來成為密文，
但是在這裡我們不需要他的加密功能，我們不用知道密文是什麼。

在這我們不記錄每個區塊的密文，我們只記錄最後一個區塊的。
可想而知，因為前面的區塊會影響後面區塊的加密結果，
這很符合MAC 所需要的訊息完整性鑑定。

GCM

同一天我們提到GCM。
GCM其實算是一種區塊密碼的操作模式，但是因為他具有 MAC 的性質，所以我把它搬來這裡講。

GCM，Galois Counter Mode，是CTR（counter mode）的擴充，需要用到 galois field 裡的乘法運算。
不果我們是老少咸宜的頻道，galois到底幹了什麼，根本不重要。

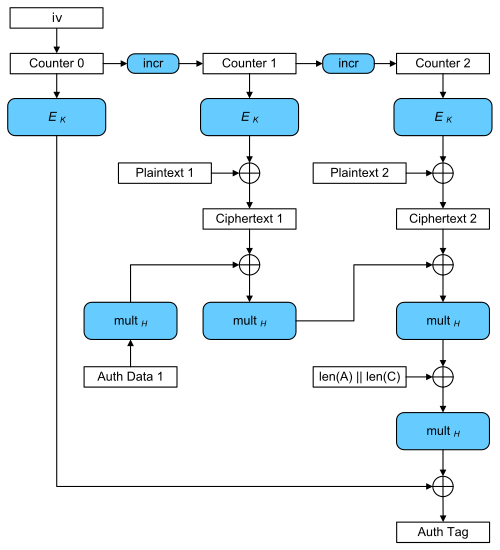
其實GCM的加密方法就跟 CTR一模一樣，只是為了達到MAC的效果，因此加上了下面的運算。

上圖中的Auth Data 是由傳送者自行設定的數字，而 H 則區塊大小位元的全 0 數字加密後的結果。
因此mult H的意思即是乘上 H 。
經過運算之後所得到的結果Authentication Tag 即是GCM的結果。
而收件者只要確認這個tag的正確性即可知道訊息的完整性。

ok以上就是今天的內容，都學會了嗎？
下次有人看到MAC只想到漢堡的時候就用這篇文教育他吧！

圖片來源：
https://comp38411.jtang.dev/docs/mac-and-hash-functions/message-authentication-code/
https://www.researchgate.net/figure/Hash-Message-Authentication-Code-HMAC-process-332-Overview-of-SHA-256-SHA-256_fig2_346634579
https://www.chegg.com/homework-help/questions-and-answers/cbc-mac-algorithm-given-lecture-notes-pictures-secure-provided-following-holds-initialisat-q45616911
https://en.wikipedia.org/wiki/Galois/Counter_Mode