今天直接動手來解題吧！
我們從根（root）開始，利用Divide and Conquer來驗證每一個子樹（Subtree），直到我們驗證到最後的葉子。

像是我們會往左驗證他的左子樹是否是BST，然後左子樹的左子樹是不是也是BST，一直到最後葉子的部分，不斷重複這些行為。

其中，我們一定要知道一件事就是：每個BST都會有一個可能的 最大值 和 最小值

像是下面這張圖的6，他的最小值就是５。
為什麼呢？因為他的父親是5。
那他的最大呢？就是他的祖先10。
所以說，因為6是在10的左子樹，所以他一定要比10小；
但他又在5的右子樹，所以他又一定要大於5。
結論就是 5 < 6 ( node.val ) < 10

如果還不清楚，我們再來看一個。
這裡的12這個左子樹，它的範圍最大值應該是15，最小值應該是 10。

以此類推的結論就是：
我們可以知道每個節點一定都有自己最大和最小的範圍，所以我們只要驗證每個節點都有在他應該有的範圍內，就可以證明他是BST了！

不過我們要怎麼去尋找他的父親跟祖父呢？
這邊我採用寫另外的helpValidateBst function來來完成，從root（10）開始追蹤 把最大值設為無限大 最小值設為負無限大，然後開始往下檢查。
每次檢查都去呼叫我們的function，並且更改 max 或 min value為我們當下的node.val

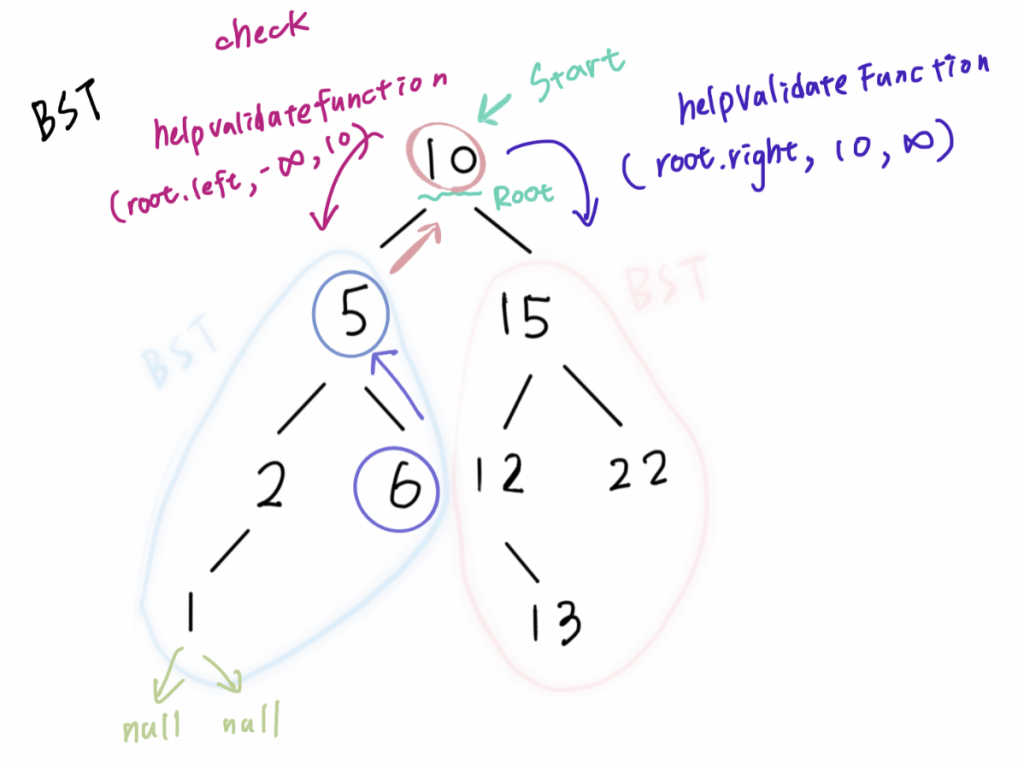
左兒子一定要小於當下node.val。
舉例：10的左邊中，因為5一定要小於10，所以我們相當於把10當作最大值傳到helper function

而右兒子一定要大於當下node.val。
舉例 10的右邊中，因為15一定要大於10，所以我們相當於把10當作最小值傳到helper function

一直檢查到最下面看到left和right都是 null 為止。
而時間複雜度的分析很明顯就是 Time = O (N)，Ｎ為我們的node數，
因為我們一定要驗證完每一個node。
而空間複雜度為O(d)，因為我們都是使用不斷呼叫function的方式，用到了stack，而d會是我們最長的branch(depth of tree)。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
const helpValidateBst = (root, minValue, maxValue) => {
	if( !root ) return true;
	if(root.val <= minValue || root.val >= maxValue) return false;
	return helpValidateBst(root.left, minValue, root.val) && helpValidateBst(root.right, root.val, maxValue);
}

var isValidBST = function(root) {
    return helpValidateBst(root, -Infinity, Infinity);
};

PS.在寫題目前一定要閱讀完整題目的定義！這一題的敘述比較嚴格的限定右子樹一定要大於root，而左子樹一定要小於root。

明日題目預告：Find the sums of the branches of a binary tree