說到廣度優先搜尋我一定要現知道Queue

Queue(佇列)是先進來的元素先出去(First In First Out = FIFO)的資料結構，通常用於讓程式具有排隊功能，依序執行工作，

而BFS使用queue來確保先被拜訪到的結點(Node)，就先成為新的搜尋起點。
以樹(tree)來說會把同一層(level)的節點拜訪完，再繼續向下一層搜尋，直到拜訪完所有節點(queue被清空為止)。

我們繼續拿DFS的圖為例
我們預期得到的結果是[ A, B, C, D, E, F, G, H, I, J, K]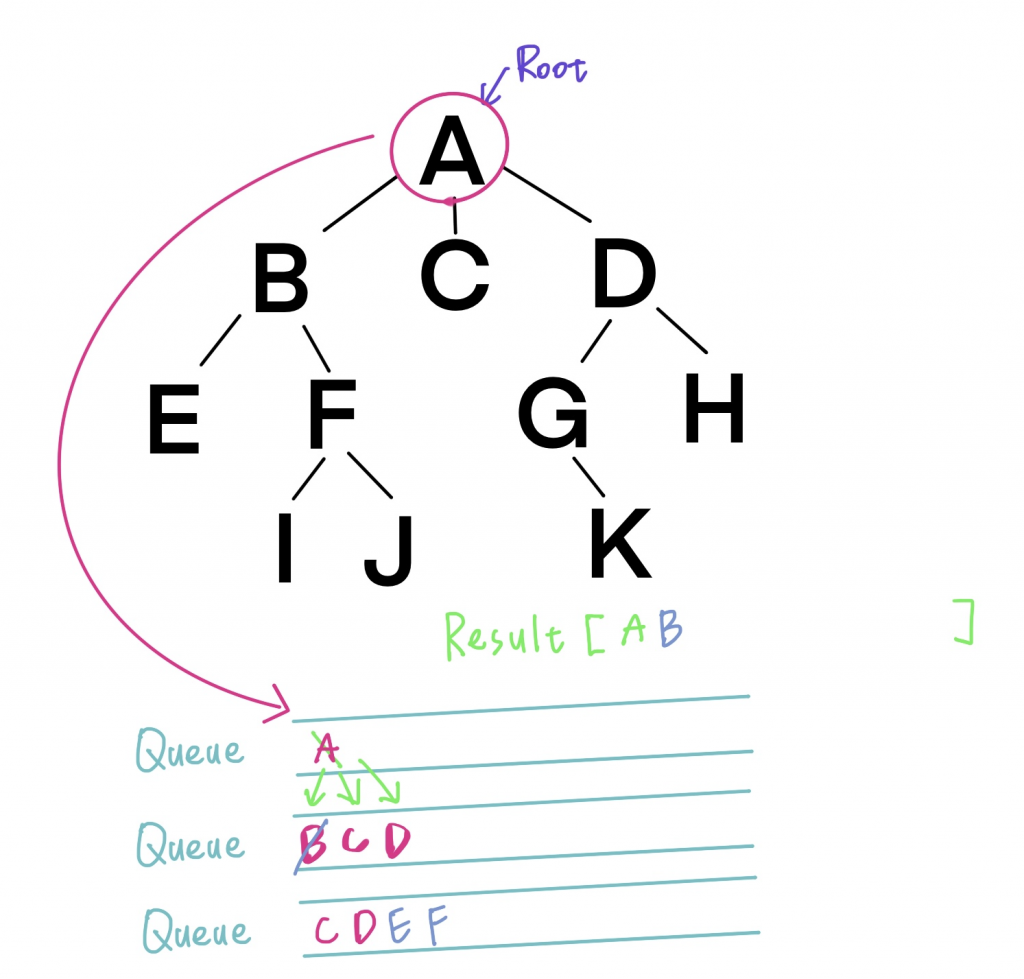

我們來看圖說故事，我們先準備Queue來讓我們的節點排隊，然後預備一個陣列來記錄結果。

首先，我們在根(Root)，也就是A開始拜訪。
我們讓A加入到我們的Queue，
這時候我們發現 「ㄟ～有人在排隊耶」！
於是我們就把它取出來，取出來卻發現他被三個小朋友給抓住了，分別是ＢＣＤ。
我們從左邊開始優先，就把ＢＣＤ加到了Queue。
最後A加到我們擺放結果的地方，結束第一回合。

接著我們來到Queue的頭，取出B，按照上面的方式，確認他有沒有被任何小朋友抓住，同樣動作：
加入Queue然後B再放入結果...

這就是我們即將用程式碼實作的流程，在實作之前，我們先來看一下時間複雜度：Ｏ(V+E) ，其中V是樹的節點樹，E則是邊數。為什麼？
我們理所當然要拜訪V個點，那E呢？
想想看我們要把一個點的小朋友都加到Queue中，那如果Ａ的小朋友直接就是ＢＣＤ我們是不是就要確認ＢＣＤ是不是有小朋友，並把他們加到Queue，那如果像是I沒有小朋友了(沒有edge) ，我們是不是就不需要再去做loop檢查的動作？
而空間複雜度:O(V)，有兩個原因：分別是儲存的結果 和 Queue(考慮最糟情況 有可的A下面剛好長滿B~K)

而今天的題目其實就是利用一樣的邏輯來實作，差別只是我們要另外把同一層的整理成一個array。
以下就是程式碼的實作

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
 
var levelOrder = function(root) {
if (!root) return [];

  const res = [];
  const q = [];
  q.push(root);

  while(q.length) {
    const lvl = [];
    const size = q.length;

    for (let i = 0; i < size; i++) {
      const node = q.shift();
      lvl.push(node.val);
      if (node.left) q.push(node.left);
      if (node.right) q.push(node.right);
    }
    res.push(lvl);
  }
  return res;
};

明日題目預告：驗證二元搜尋樹Validate Binary Search Tree
講了幾天的樹，當然不可以忽略這一題！