Chap.II Machine Learning 機器學習

https://yourfreetemplates.com/free-machine-learning-diagram/

Part 5. Imbalanced Data 不平衡資料

專案中，常會遇到 Imbalanced Data 不平衡資料。
如：乳癌患者、恐怖份子查驗、詐欺犯預測...等，我們關注的是＂少數＂樣本是否能被準確預測？

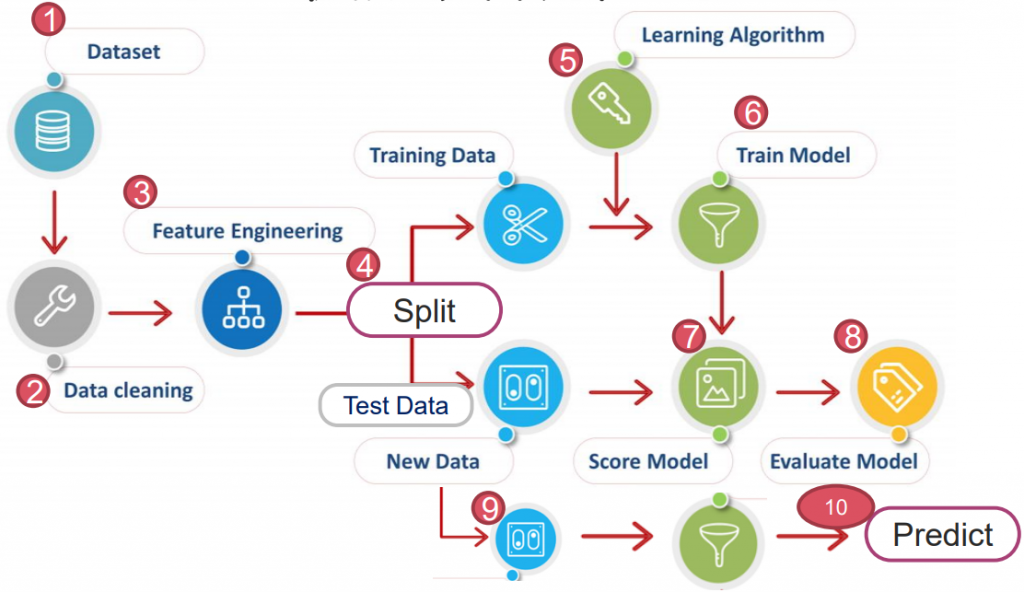
以蛋白質範例，可以發現決策邊界完全無法將少數資料分離。

sns.set(style='white')

ds = fetch_datasets()['protein_homo']

X = PCA(n_components=2).fit_transform(ds.data)
X = MinMaxScaler().fit_transform(X)
y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42, shuffle=True)

# print('X shape:', X.shape)
# print('y shape:', y.shape)
# print('Positive Ratio:', np.count_nonzero(y==1) / y.shape[0])

lr = LogisticRegression().fit(X_train, y_train)
y_pred = lr.predict(X_test)

# print('Report :', classification_report(y_test, y_pred))
# print('ROC :', roc_auc_score(y_test, y_pred))

plot_x = np.linspace(0, 1, 1000)
plot_y = (-lr.coef_[0][0] * plot_x - lr.intercept_) / lr.coef_[0][1]

# 作圖
sns.scatterplot(X_train[:, 0], X_train[:, 1], hue=y_train)
plt.plot(plot_x, plot_y)
plt.title('Imblanced Data: Original')
plt.ylim(0, 1.5)

plt.show()

為了解決此問題，可透過以下方式：

5-1. 評估指標

一般來說 Accuracy 準確度是一個直覺性高的指標。
但單純的準確度並沒辦法精準衡量模型是好是壞，因此這裡介紹幾種更常見的評估方式：

A. Confusion Matrix 混淆矩陣

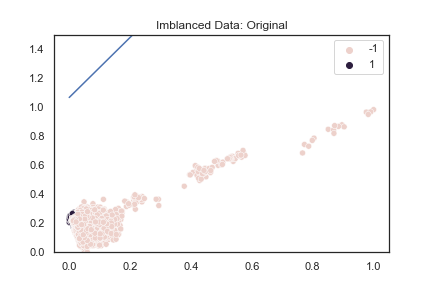
下圖為上述資料的混淆矩陣，可發現準確率達到 47700 / (47700+398) = 99.2%

from sklearn.metrics import plot_confusion_matrix
cm = plot_confusion_matrix(
    lr,
    X_test, y_test,
    cmap=plt.cm.Blues
)
plt.show()

然而正樣本的精確率卻是 0 %，意味模型根本無法辨別正樣本。

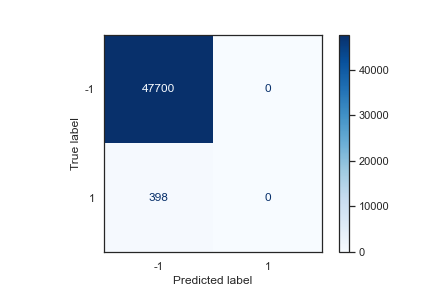
甚麼是精確率？

B. Precision and Recall 精確率與召回率

Precision 精確率：被＂預測正確樣本＂中，是＂實際正確樣本＂有多少比例。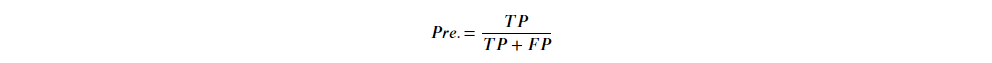

Recall 召回率：＂實際正確樣本＂中，被＂預測正確樣本＂有多少比例。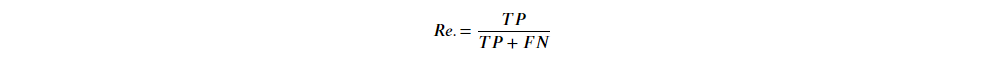

有了精確率與召回率，統計學家進一步定義了：

C. F1 score

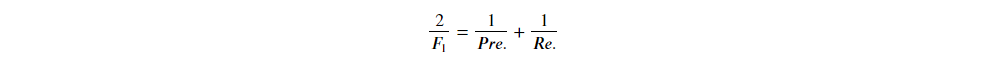
化簡後可得：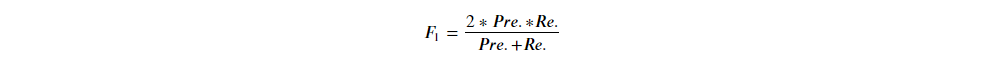

也有學者提出精確率 & 召回率不同權重的算法：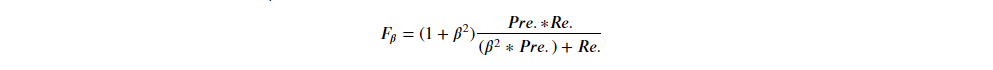

D. ROC 接收者操作特徵曲線

全名 Receiver Operating Characteristic，而曲線下面積稱 Area Under Curve (AUC)。

首先定義：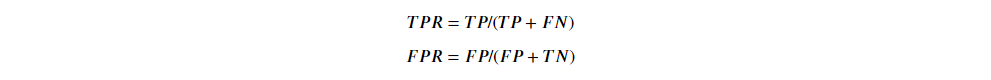

有了這兩個指標，再配合模型的＂閾值＂，我們可以畫出一條 ROC 曲線。

什麼是閾值（Threshold）？

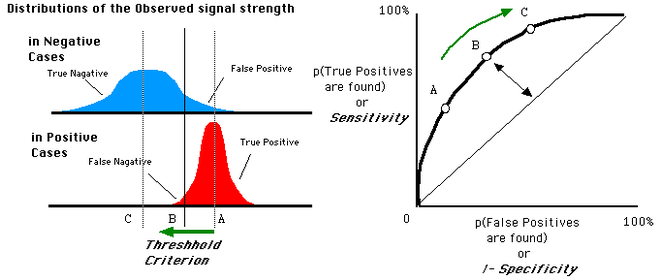
圖左：
藍色為負樣本，紅色為正樣本，橫軸則是模型預測的機率。
很直覺的理解：正樣本集中於預測機率高的分段上，負樣本則較低。
此時我們可以設一個＂閾值＂（通常預設 0.5），以上判定為正，以下判定為負。

圖右：
將橫軸設為 FPR，縱軸設為 TPR，配上不同閾值可畫出一條曲線。
若選 A 點作閾值，則大部分負樣本都被剔除，但正樣本也留下較少（TPR/FPR 皆下降）。
約有一半的正樣本被判定為正，TPR ≈ 0.5 ，少部分負樣本被判定為正，FPR ≈ 0.2 ，
最終得到 A 點在右圖曲線上的位置。

AUC 就是計算曲線下的面積，其越大表示模型越好。

1. 若 ROC=0.5，曲線=對角線，模型沒有鑑別度。不管正樣本判正比例多高，都伴隨同比例的負樣本被錯判。
2. 若 ROC=1，則是一完美分類的模型！100% 成功預測出正樣本的同時還沒有任何的負樣本被分類錯誤。
   

蛋白質範例的 ROC（AUC）：

from sklearn.metrics import roc_curve, roc_auc_score

fpr, tpr, threshold = roc_curve(y_test, y_pred)
auc = roc_auc_score(y_test, y_pred)

plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, c='b', label=f'AUC = {auc:0.2f}')
plt.plot([0, 1], [0, 1], 'r--')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.legend(loc='best')

plt.show()

至此，我們可用更科學的方法來判斷模型好壞了！

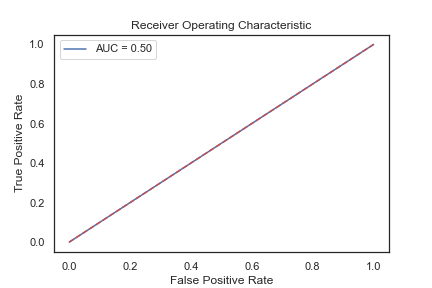
但問題仍沒解決：樣本比例差異過大的情況下，總會使訓練的模型判斷能力差。
因此，接下來我們會嘗試透過採樣技術來克服它。

5-2. 重組資料

將少數樣本用某種方式重複抽樣或合成新樣本，稱過採樣。
相反，將多數樣本中較不具代表性的移除以免造成雜訊，稱欠採樣。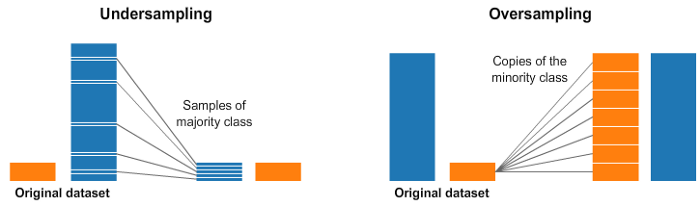

A. Oversampling 過採樣

A1. SMOTE

全名 Synthetic Minority Oversampling Technique 合成少數過採樣技術。
概念是在少數樣本位置近的地方，人工合成一些樣本。

A. 挑一個少數派（紅點），並將鄰近的 k 個（k=3）點找出。（Pic1）
B. 從 k 個近鄰點中隨機選取一個，透過公式合成 N 個（N=3）樣本點。（Pic2）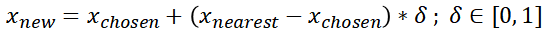

C. 接著對所有的少數點做同樣的操作。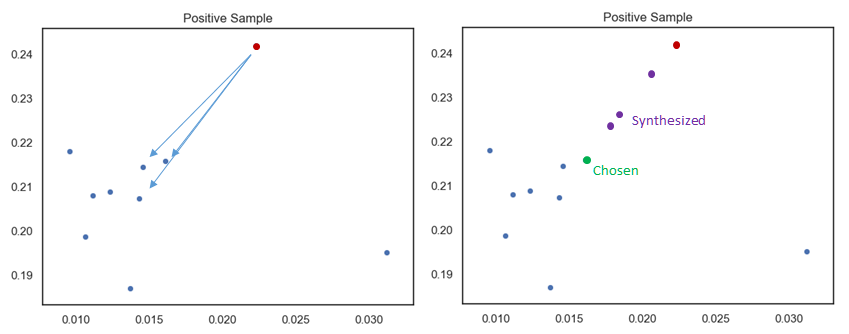

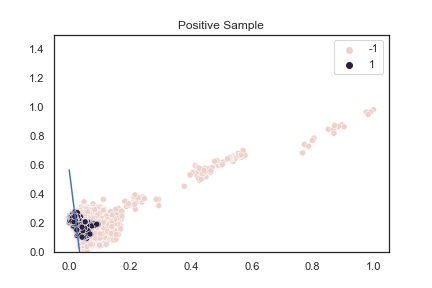
蛋白質範例操作 SMOTE：

from imblearn.over_sampling import SMOTE
from sklearn.metrics import roc_auc_score, classification_report

X_re, y_re = SMOTE(random_state=42).fit_resample(X_train, y_train)

lr = LogisticRegression().fit(X_re, y_re)
y_pred = lr.predict(X_test)

plot_x = np.linspace(0, 1, 1000)
plot_y = (-lr.coef_[0][0] * plot_base - lr.intercept_) / lr.coef_[0][1]

# 作圖
sns.scatterplot(X_re[:, 0], X_re[:, 1], hue=y_re)
plt.plot(plot_x, plot_y)
plt.title('Positive Sample')
plt.ylim(0, 1.5)

plt.show()

結合剛剛的 ROC（AUC）曲線：

from sklearn.metrics import roc_curve, roc_auc_score

fpr, tpr, threshold = roc_curve(y_test, y_pred)
auc = roc_auc_score(y_test, y_pred)

plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, c='b', label=f'AUC = {auc:0.2f}')
plt.plot([0, 1], [0, 1], 'r--')
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.legend(loc='best')

plt.show()

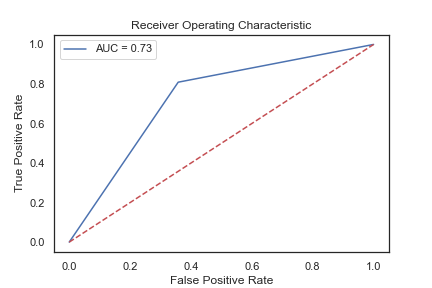
print(auc)

>>  0.7254869736523286

ROC 顯著提升（50% → 72%）！！！

A2. Border Line SMOTE

SMOTE 雖不錯，但有一個明顯缺點：對＂所有少數樣本＂都做過採樣。
大多時候並不是所有少數樣本都無鑑別度，真正無鑑別度的是與多數樣本混合在一起的少數樣本。

靠近邊界的少數樣本因與多數樣本混合在一起，易產生雜訊。若對邊界樣本學習，可能將多數樣本誤判為少數。
因此，對 SMOTE 算法做出改進的算法，即 SMOTE Border Line。

from imblearn.over_sampling import BorderlineSMOTE
blsmote = BorderlineSMOTE(random_state=42, kind=’borderline-2')
X_re, y_re = blsmote.fit_resample(X_train, y_train)

實作上，其實還是更常使用 SMOTE，畢竟 Borderline 方法的計算複雜，且閾值設定也缺乏公定的標準。
需要花更多時間調參，然而跑分進步幅度卻不大。

B. Undersampling 欠採樣

相對過採樣，欠採樣是將多數樣本進行 Scale Down，使模型的權重改變，少考慮一些多數樣本。
最簡單的做法是隨機排除掉一些多數樣本。但有可能排除掉邊界樣本，
使沒鑑別度少數樣本也被模型考慮，雖使鑑別度上升，卻增加過擬合風險。

B1. Tomek Link

會針對所有樣本去遍歷一次。
令兩個樣本點 x, y 分屬不同的 class，一個為多數樣本，另一為少數，可計算樣本間距 d(x, y)。
若找不到第三個樣本點 z，使得任一樣本點到 z 的距離比樣本點間距還小，則刪去其。

核心理念：找出邊界鑑別度不高的樣本，認為這些樣本屬雜訊應該剔除（類似 Borderline SMOTE）。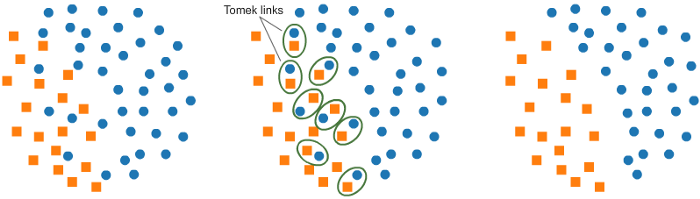

蛋白質範例操作 SMOTE + TomekLinks：

X_re, y_re = SMOTE(random_state=42).fit_resample(X_train, y_train)
X_rere, y_rere = TomekLinks().fit_resample(X_re, y_re)

lr = LogisticRegression().fit(X_rere, y_rere)
y_pred = lr.predict(X_test)

from sklearn.metrics import roc_curve, roc_auc_score

fpr, tpr, threshold = roc_curve(y_test, y_pred)
auc = roc_auc_score(y_test, y_pred)
print(auc)

>>  0.7332799742949548

可以發現此例中，結合欠採樣後並沒有讓 AUC 顯著提升（72% → 73%）。

故專案中通常以過採樣為主，欠採樣為輔去進行資料重組。

B2. Edited Nearest Neighbor

與 Tomek Links 觀念相同，也是透過某種方式來剔除鑑別度低的樣本。
ENN 改成對多數樣本尋找 K 個近鄰點，若一半以上（門檻可自設）不屬於多數樣本，就將該樣本剔除。

5-3. 注意事項

實作上，其實很常同時使用過採樣 + 欠採樣來做資料重組。如下圖：

A. 先切分資料，再對訓練資料採樣。

重新採樣的目的是讓模型產生鑑別度，而不是讓模型學習錯誤資訊。若先採樣才切分，可能使測試資料偏離了原資料，導致模型學習到一堆雜訊。

B. 常透過交叉驗證控制過擬合。

不管哪種採樣，都會大幅增加過擬合程度（如：樣本數少，又做欠採樣）。
即使模型區分出來，由於欠採樣後多數樣本過少，導致模型只側重學習某部分樣本，無法反映資料全貌。
此時，交叉驗證、建立多模型做集成學習，都會是好的解決方式。

C. 觀察少數樣本與多數樣本分布情形。

蛋白質範例是因為少數樣本與多數樣本看上去還能分離，實際運行很有可能碰到完全分不開的例子。
若少數樣本雜亂地散落在多數樣本之間，此時就不要考慮採樣問題。
可以優先評估是否資料本身的分佈有問題，像是一開始回收數據錯誤，或樣本並非歐幾里得分布等情況。

結論：

1. 面對不平衡資料，需改變判斷標準，而不能僅用＂準確率＂判定模型。
2. 若發現 F1 score、ROC 過低，需觀察資料分布，才考慮使用過採樣/欠採樣技術。
3. 若有採樣，需使用交叉驗證控制過擬合。
   .
   .
   .
   .
   .

Homework Answer：

使用內建 wine，試著用 pipeline、Cross Validation，寫個迴圈以操作演示過的演算法。

import numpy as np
import pandas as pd
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

ds = load_wine()

X = pd.DataFrame(ds.data, columns=ds.feature_names)
y = pd.DataFrame(ds.target, columns=['Wine'])


X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# 把要用的 model 整理出
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import RandomForestClassifier

models = []
models.append(("Logistic Regression", LogisticRegression()))
models.append(("Naive Bayes", GaussianNB()))
models.append(("K-Nearest Neighbour", KNeighborsClassifier(n_neighbors=3)))
models.append(("Decision Tree", DecisionTreeClassifier()))
models.append(("Support Vector Machine-linear", SVC(kernel="linear")))
models.append(("Support Vector Machine-rbf", SVC(kernel="rbf")))
models.append(("Random Forest", RandomForestClassifier(n_estimators=7)))

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import StratifiedKFold
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

scores = []
names = []
for name, model in models:
    
    kfold = StratifiedKFold(n_splits=10).split(X_train, y_train)
    
    rfc_PL = make_pipeline(
    StandardScaler(),
    PCA(n_components=2),
    model
    )
    
    cv = cross_val_score(rfc_PL, X_train, y_train, cv=kfold, scoring = "accuracy")
    names.append(name)
    scores.append(cv)

for i in range(len(names)):
    print(f'{names[i]:<30}: {scores[i].mean()*100:.3f}')
    
>>  Logistic Regression           : 96.090
    Naive Bayes                   : 96.090
    K-Nearest Neighbour           : 92.949
    Decision Tree                 : 94.551
    Support Vector Machine-linear : 95.321
    Support Vector Machine-rbf    : 96.090
    Random Forest                 : 96.090

文章參考