幾何轉換(Geometric Transformations) 是常用的數位影像處理技術，主要作用為｢改變數位影像中的像素空間，但不改變其灰階或色彩值。」

1.空間轉換
介紹幾何轉換前，首先定義空間轉換的方法:
空間轉換可以定義為 ，其中，(x,y)為輸入影像的座標，(x',y')為輸出影像的座標，T稱為空間轉換函數

空間轉換的方法包含正向映射(Forward Mapping)與反向映射(Inverse Mapping)，兩者關係如下圖:

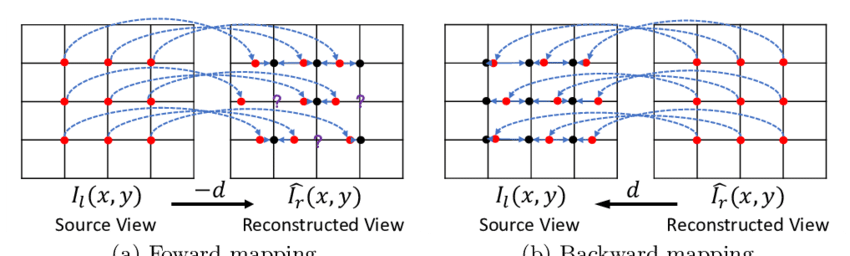
正向映射主要是根據輸入影像的空間座標(x,y)以及轉換函數T，計算輸出影像映射的空間座標(x',y')，也就是說:

再將輸入影像的灰階或色彩值複製到輸出影像。此方法雖然簡單直接，但在進行一些操作的時候，例如放大兩倍等等，可能會有部分輸出影像的像素無直接對應的像素，造成影像的破洞。比如將一個影像放大兩倍，輸入影像座標(0,0)的像素會被映射到輸出影像像素(0,0)、(0,1)被映射到(0,2)，可是輸出影像(0,1)和(0,5)等位置沒有直接對應的像素，因此會產生破洞問題。

**反向**映射與正向相反，根據輸出影像座標(x',y')以及反轉換函數T'計算其在輸入影像的座標，也就是說:

再將原始影像灰階或色彩值複製到輸出影像，這樣的方法就不會產生上述的破洞問題，因此實際運用上會以反向映射為主。

2.影像內插
無論採用正向或反向映射，在決定輸出影像像素的灰階色彩值，有可能發生無法對應到整數空間座標的情形，又或是假設今天你電腦或手機螢幕的解析度為2K，但要撥放的影片解析度只有Full HD，那這種情況要怎麼辦呢?此時即就需要內插法(Interpolation)處理。

以下介紹幾種常見內插法，包含:最鄰近內插法(Nearest Neighbor Interpolation)、雙線性內插法(Bilinear Interpolation)、雙立方內插法(Bicubic Interpolation)。

2-1 最鄰近內插法
最鄰近內插法是最簡單的方法，也稱為零揭內插法(Zero-Order Interpolation)。這方法是根據離映射點最近的空間座標像素取其灰階值或色彩值，如下圖所示: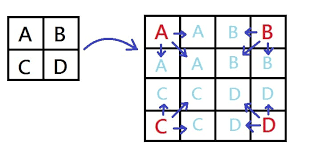

當要放大的倍率越多，可以明顯的發現此方法的效果就越差，就會產生有些地方會有馬賽克一格一格的效果。

2-2 雙線性內插法
此方法又稱為二階內插法(Second-Order Interpolation)，既然上一個方法只參考最近的像素，那麼這次我們就參考四週頂點的像素，並依據距離的權重來決定我們要的值。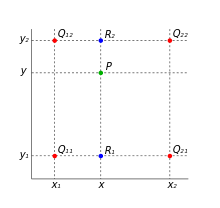

如上圖所示，欲求P(x,y)，可以先參考P點四週的頂點位置，

且

則

雙線性內插法由於其計算複雜度不高、效果也不錯，因此是蠻實用的內插法。

2-3 雙立方內插法
又稱為三階內插法(Third-Order Interpolation)，看到三階這個詞可以發現這是從上一個內插法演變而來，這次參考四週16個點的像素值，因此計算複雜度變得更高了。

此方法的計算量大，由於參考點更多，可以保留較精確的影像細節品質，但在即時影像處理較不實用。

除了上述幾個典型的內插法，OpenCV本身也提供更高階的方法，例如Lanczos 8 * 8 內插法、反混跌(Anti-Aliasing)等等，這些方法的計算量相對來說也比較大，因此通常不會採用。