今天再來一天Stack，昨天說到Stack的應用有很多種，今天就來舉幾個實例給大家看吧ξ( ✿＞◡❛)▄︻▇▇〓▄︻┻┳═一

Stack Permutation

定義:

給予n個data依序push入stack，在中間過程中，可執行任意的合法之pop將資料輸出。依此模式下所產生的所有輸出之排列組合，稱之。

例:給abc，列出所有stack permutation

我們先把abc排列的所有組合寫出來(3!個=6個)，嘗試看看能不能實做出來

可以判斷誰一定不能在誰的前面，用刪去法!

1. abc : push a, pop, push b, pop, push c, pop
2. acb : push a, pop, push b, push c, pop, pop
3. bac : push a, push b, pop, pop, push c, pop
4. bca : push a, push b, pop, push c, pop, pop
5. cab : 無法產生
6. cba : push a, push b, push c, pop, pop, pop

n個data之stack permutation個數

公式 : 1/n+1 * C(2n,n)
例如:n=3 ⇒ 1/3+1 * C(6,3) = 5

n個data之stack permutation個數
= n個nodes可以形成的不同二元樹之個數
= n個"("與n個")"之合法配對個數
= (n+1)個矩陣香澄枝所有乘法組合方式數目

Infix轉Postfix/Prefix

###比較
/ | Infix | Postfix | Prefix
------------- | ------------- | -------------
格式 | operand1 operator operand2 | operand1 operand2 operator | operator operand1 operand2
例子 | a+b , a-b , (a-b)/c | ab+ , ab- , ab-c/ | +ab , -ab , /c-ab

Infix轉Postfix之演算法

While(Infix 尚未由左而右scan完)
{
    x=NextToken(Infix);
    if(x=operand) then print(x);
    else if(x= ")" ) then
        repeat
            y=pop(S);
            if(y!= "(" ) then print(y);
        until (y== "(" );
    else
        switch(比較優先權(x,S.Top)
        {
            case">":push (S,x);
                    break;
            case"<=":
                    repeat
                        y=pop(S);
                        print(y);
                    until(x>S.Top);
                    push(S.x);
        }
    }
    while(not Isempty(S))
    {
        y=pop(S);
        print(y);
    }//清光stack S並列印

實際例子用Stack畫出Infix轉Postfix

題目:a*(b+c/d)-e

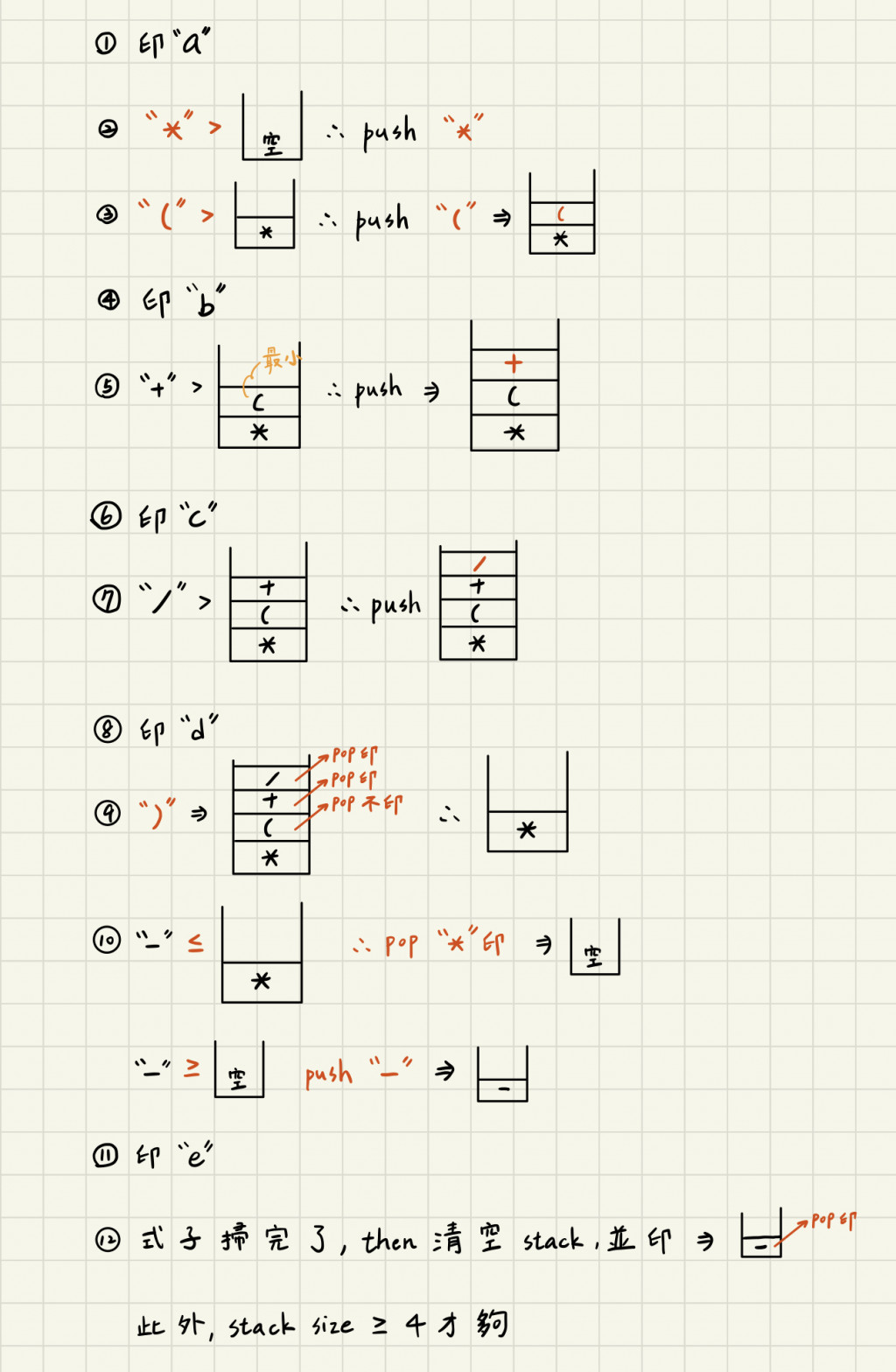
output：abcd/+*e-

Compiler之parsing

例:

寫出一演算法判斷輸入的括號配對字串是否正確，正確回傳Yes，否則回傳No

觀念

字串仍未Scan完
"(":push(S,x)
")":if Isempty(S) then return "No" ➝ ")"數多於"("數
pop(S);
已經Scan完
if Isempty(S) return "Yes"
else return "No" ➝ "("數目大於")"

eg.正確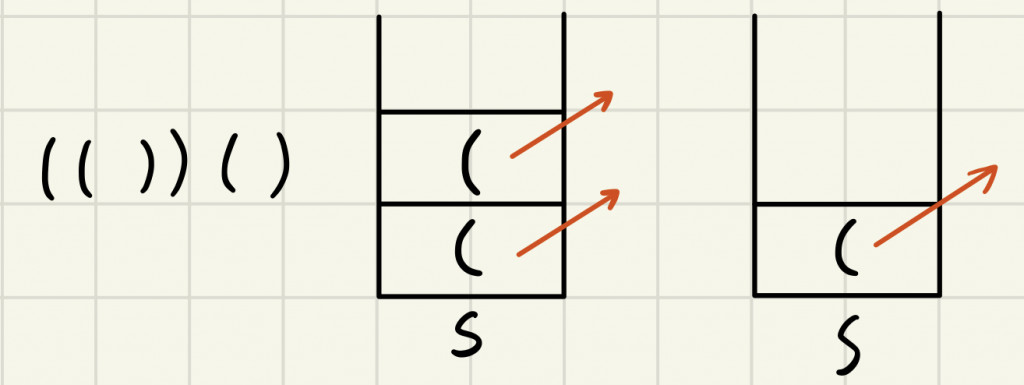

eg.不正確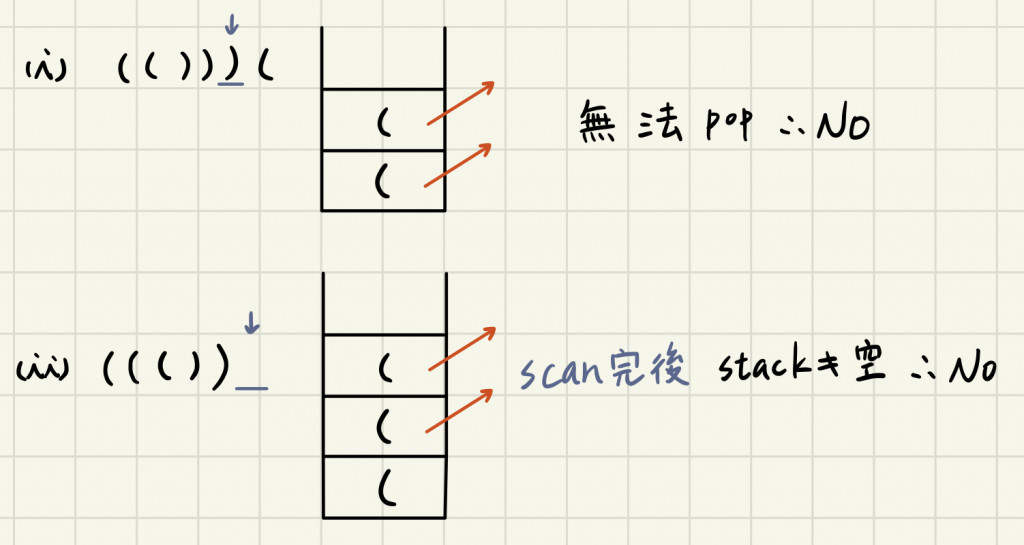

演算法

{
    while(輸入字串尚未Scan完)
    x=NextToken(字串);
    if(x== "(" then push(S,x);
    else if(x== ")" )then
    {
        if Isempty(S) then return "No"; //不合法，要pop但stack為空
        pop(S);
    }
    if Isempty(S) then return "Yes";
    else return "No"; //不合法，Scan完但Stack內還有東西
}