Intro

Earlier, we learned about the application of loops, which continuously execute block programs through conditional judgments. The concept of recursion is somewhat similar.

Recursion, as the name suggests, is a technique in which a function calls itself and passes its return value as a new argument. One advantage of this technique is that it can solve complex problems that are difficult to handle in loops, such as the halting problem in this chapter and the classic problem of the Hanoi Tower, which will be introduced in the next chapter. However, the most important thing to note when using recursion is the number of times it is recurred. We usually call it “depth”.

The most criticized aspect of recursion is that too many calls themselves can cause the return value to be difficult to control. Although concise code greatly increases readability, not providing an exit from the call will make the program difficult to understand.

Before the formal introduction, here is a brief example of using recursion to calculate factorials:

public int fac(int num) {
    if (num != 1) {
      return num * fac(num-1);         
    } 
		else
	    return 1;
}
public class void main(String[] args){
	System.out.println(fac(4));           //求 4! = 24
}

• Program analysis: The argument 4 is passed in, and the first condition of the function is judged. Then, the function calls itself again, passing in 3, and the original 4 is stored in memory, waiting for the final return 1 → to start multiplying one by one.
  

Recursion

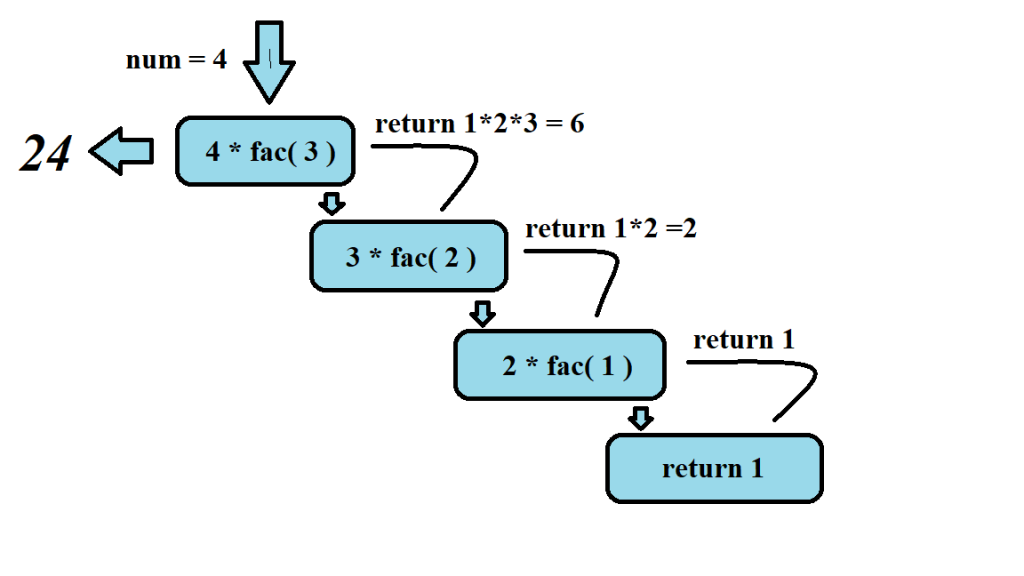
Let's explain it by listing the patterns of recursive formulas again:

public static int sum(int k) {
    if (k > 0) {
      return k + sum(k - 1);         //Using sum(k-1) calling itself repeatly 
    } 
    else {
      return 0;
	}
}

Suppose we pass in 20, the function will execute successive recursions until k ≤ 0.

20 + sum(19)
20 + ( 19 + sum(18) )
20 + ( 19 + ( 18 + sum(17) ) )
...
20 + 19 + 18 + 17 + 16 + 15 +14 + … + sum(0)
20 + 19 + 18 + 17 + 16 + 15 +14 + … + 0 = 210

• By listing the method, we can see that in fact, when the compiler executes recursion, it first stores the initial number, and the subsequent numbers are placed on top of the previous number. Finally, it takes the top value and returns it one after the other until it reaches the answer we want. This structure is called a stack.
  

Halting Condition

It's like a loop. If we don't set a stopping condition for it, it will form an infinite loop, and the screen will keep running without stopping...
Recursion. We call this the “halting condition”. It determines when recursion halts.

static int sum(int start, int end) {
    if (end > start) {
      return end + sum(start, end - 1);     
    } 
	else {
      return end;
    }
  }

• Program analysis: Suppose we pass in start = 10 and end = 20. This example will perform a 10-20 concatenation, and the stop condition occurs when the end parameter is finally saved with 10. Only the value 10 will be returned, stopping the execution of this recursion. This is what we call a stop problem.