Day 19 - 分類(Classification)介紹與實作

14th鐵人賽

dengliu2000

2022-10-03 23:11:19

619 瀏覽

分享至

昨天的文章中主要提到了回歸的部分,它是屬於監督式學習中的一個類型,而今天的文章中我主要想提一下監督式學習中的另一個部分,那就是分類的部分.在分類的問題中,我們期望可以找到一個符合資料分佈的函數,如果能順利找到一個能將不同種類的資料分得很好,那麼往後要是有一筆新的資料進入,就能利用函數判斷它所座落的區域,並成功判別新資料的種類.

分類模型

二元分類(binary)
多分類(Multi-Class)

分類問題是屬於監督式學習的範疇,在資料有被標籤(labeled)的情況下,透過分類模型可以找出明確的劃分線,將不同標籤類別區分出來.

以PyTorch實作分類模型(以不同顏色的點來呈現並計算準確度)

建立資料集

import torch
import matplotlib.pyplot as plt

n_data = torch.ones(100, 2)
x0 = torch.normal(2*n_data, 1)
y0 = torch.zeros(100)
x1 = torch.normal(-2*n_data, 1)
y1 = torch.ones(100)

x = torch.cat((x0, x1), 0).type(torch.FloatTensor)
y = torch.cat((y0, y1), ).type(torch.LongTensor)

plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

建立神經網路

import torch
import torch.nn.functional as F

class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.out = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):
        x = F.relu(self.hidden(x))
        x = self.out(x)
        return x

net = Net(n_feature=2, n_hidden=10, n_output=2) 

print(net)

訓練網路

optimizer = torch.optim.SGD(net.parameters(), lr=0.02)

loss_func = torch.nn.CrossEntropyLoss()

for t in range(100):
    out = net(x)

    loss = loss_func(out, y)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

可視化訓練過程

import matplotlib.pyplot as plt

plt.ion()
plt.show()

for t in range(100):

    ...
    loss.backward()
    optimizer.step()

    if t % 2 == 0:
        plt.cla()
        prediction = torch.max(F.softmax(out), 1)[1]
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
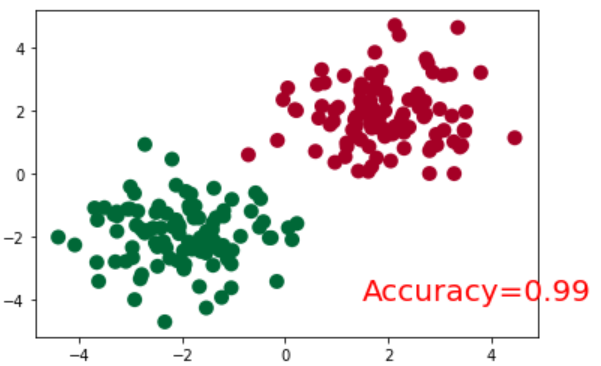
        accuracy = sum(pred_y == target_y)/200.
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()
plt.show()