前言

本章節要談的是 Leftist Heap，會先從緣由開始讓大家開始了解。此外，會先有一些先備知識要先知道，才能來定義Leftist Heap，不過不用擔心，這邊都會提！

緣由

為了改善 merge 2 Heap 的時間才出現的，我們來回想一下，以前在 Heap 章節，談到合併兩個 Heap 的方法，是透過將兩個 Heap 所有資料放在 Array 中，再來進行 Bottom-up 的建置，時間會是 O(n)
而 Leftist Heap 能夠把合併時間降到 O(logn) !

先備知識

shortest(x)

我們先來定義何謂 Shortest(x)
若 x 是 extended B.T 中的任一點，則其為

• 0, 如果是外部節點
• 1+min{shortest(x's lchild), shortest(x's rchild)}, 若其為內部節點

Leftist Tree

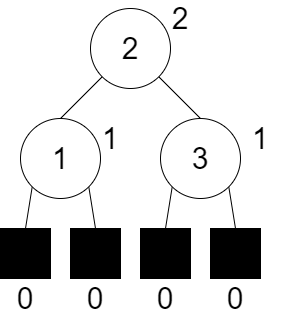
針對 extended B.T 中所有內部節點 x
其 shortest( x 的左子點) ≥ shortest( x 的右子點)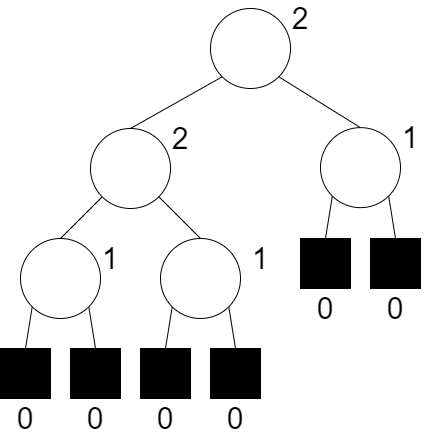

定義 Leftist Heap

假設我們以 Leftist min Heap 為例，我們可以定義 leftist heap 是
1. Leftist tree
2. min tree (all parent ≤ child)

所以我們也可以稱之為 min Leftist Tree

Merge

現在就來講最重要的 merge

1. 先比較 H1 and H2 root 找出 min
2. 假設 H1 的 root 較小，便將 H1 root 設定為新 root 並保留左子樹
3. 然後把右子樹跟 H2 Root 比較，小的放入右子樹
4. 重覆成為一個 min tree
5. 檢查是否符合 leftist tree 性質，不符合就做SWAP(左右子樹)