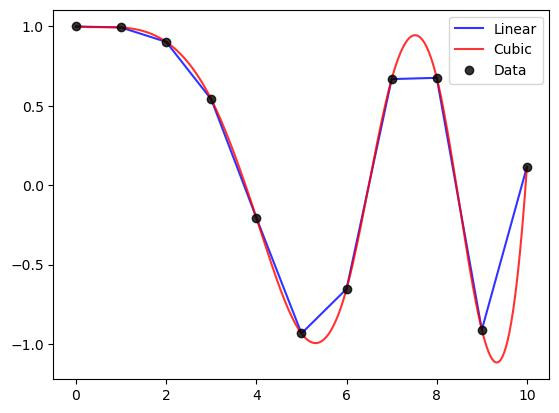
當我們需要將有序資料點視覺化，甚至是估計點之間的數值時，我們會使用內插（Interpolation）。最簡單的方式就是用直接做線性內插，不過得出來的結果就是很粗糙的直線。如果要得到連續且平滑的內插值，則會需要用到曲線去做內插，比較常見的方法是用二次或三次函數。

使用Scipy即可輕鬆的實現各種曲線內插：

from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import numpy as np


# Pseudo data
x = np.linspace(0, 10, 11)
y = np.cos(-x**2/9.0)

# Cubic spline interpolation
x_fine = np.linspace(0, 10, 1000)
f_interpolate = interp1d(x, y, kind='cubic')
y_fine = f_interpolate(x_fine)

# Plot
plt.plot(x, y, 'b-', alpha=0.8, label='Linear')
plt.plot(x_fine, y_fine, 'r-', alpha=0.8, label='Cubic')
plt.plot(x, y, 'ko', alpha=0.8, label='Data')
plt.legend()
plt.show()

本篇筆記使用Numpy去實作一個三次樣條內插（Cubic Spline Interpolation）的算法，並著重於步驟思路演示。

原理

和線性內插一樣，兩個資料點間會決定一條線段，所以如果今天有n個資料點，就會有n-1條線段，而在三次內插中，每一條線段是由三次多項式代表，如第i條線段表示為：

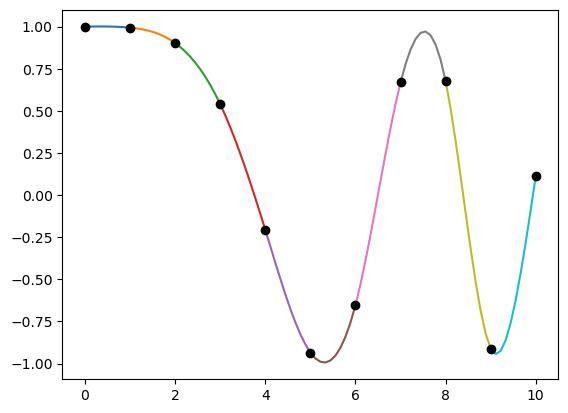
▲兩個點之間的線段都是不同的三階多項式

我們接下來要做的事，就是解出所有線段的係數才能夠得到線段的函式。一個三次多項式中會有4個未知數，也就是abcd，而假設我們有n筆資料，就會有n-1條線段，總共就會有4(n-1)個未知數，也就是說我們會需要4(n-1)條方程式去解所有未知數。
為演示方便起見，這裡設一個n=3的例子：x = [0, 1, 2], y = [1, 3, 2]

所以我們就會有兩條線段：

條件一：端點

最簡單的條件就是我們知道線段的左右兩端一定要黏在點上，所以每個線段可以產生出2個條件，如此我們可以得到2(n-1)個方程式。

左端：

右端：

條件二：平滑

接下來我們還要考慮一件事情，就是兩個線段連接處要連續且平滑，這個條件透過微分達成。兩個線段在同一點微分相等就代表在該點時斜率會相同，所以就會有“平”的結果，而如果要“滑”的話，我們就可以進一步用二階微分，讓該點處的斜率變化量相等而更圓滑。兩個線段可以提供1個微分等式，因此一階微分可以提供n-2個條件，二階微分也提供n-2個，共有2(n-2)個條件。

一階微分

二階微分

那既然可以用二階微分，那可否使用三階甚至四階微分呢？可以這麼想，三次多項式在二階微分後，會變成一條直線，而兩條直線在資料點上本質上就會是個折點，會跟平滑矛盾，所以在三次多項式三階微分以上的條件都是沒有幾何意義的。

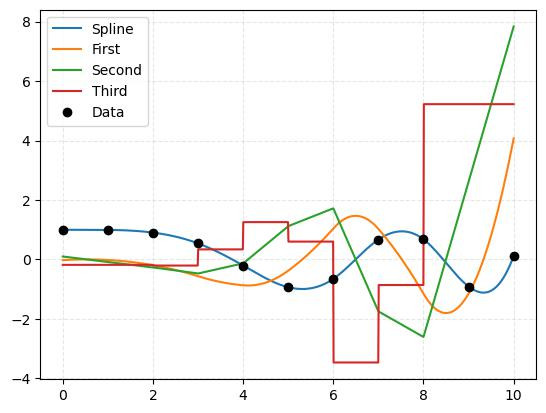
▲三階微分（Third）幾何上就不會連接起來

條件三：邊界

那麼有了前兩個條件一共4n-6個方程式，就還缺2個條件，而剩下這兩個條件的花樣就多了，根據不同的設計可以得到不同的幾何效果。就以Scipy的scipy.interpolate.CubicSplineAPI來說，就提供了not-a-knot、periodic、clamped、natural，後面的筆記會各別簡介，大致上都是拿頭和尾的2條線段做操作，畢竟剛剛找微分條件的時候，第一個和最後一個資料節點沒有做出貢獻嘛。以下會拿natural做演示。
natural的方法就是把頭跟尾2線段，做二階微分然後讓它等於0。這在幾何意義上是什麼意思呢，簡化來說就是末端線段接到節點時，會接近一條直線，不會有曲線的情形。有興趣深入探討的話，可以到維基百科查閱反曲點。

邊界條件

求解

至此，我們終於集齊4(n-1)個龍珠方程式啦！不過在求解之前，我們要先將上面那一大坨方程式整理成矩陣形式。矩陣雖然是個很反人類的數學符號，但和電腦卻是很情投意合呢。

矩陣形式

而要求解其實只需要算出矩陣A的反矩陣，此筆記會使用Numpy去處理。

程式

步驟

在編寫程式碼之前，先把大致要做的步驟列出來：

1. 收集端點相等的方程式
   • 左端
   • 右端
2. 收集二階導數的方程式
3. 收集三階導數的方程式
4. 收集邊界條件的方程式
5. 矩陣求解
6. 計算曲線內插

Numpy演示

import matplotlib.pyplot as plt
import numpy as np


# Cook pseudo data
x = np.linspace(0, 10, 11)
y = np.cos(-x**2/9.0)

# Sure the sequence is sorted by x
sort_i = np.argsort(x)
x = x[sort_i]
y = y[sort_i]

# 4*(n-1) unknown variables
n = len(x)
# Ax = b
matrix = []  # A
target = []  # b

# (1) Endpoint equality: 2*(n-1) equations
for i in range(n-1):  # n-1 curves
    for j in range(2):  # left and right
        row = np.zeros(4*(n-1))
        row[4*i:4*i+4] = np.array([x[i+j]**3, x[i+j]**2, x[i+j], 1])
        matrix.append(row)
        target.append(y[i+j])

# (2) First derivative equality
for i in range(n-2):  # n-2 equations
    row = np.zeros(4*(n-1))
    row[4*i:4*i+8] = np.array([3*x[i+1]**2, 2*x[i+1], 1, 0] + [-3*x[i+1]**2, -2*x[i+1], -1, 0])
    matrix.append(row)
    target.append(0)

# (3) Second derivative equality
for i in range(n-2):  # n-2 equations
    row = np.zeros(4*(n-1))
    row[4*i:4*i+8] = np.array([6*x[i+1], 2, 0, 0] + [-6*x[i+1], -2, 0, 0])
    matrix.append(row)
    target.append(0)

# (4) Boundary condition
# the leftmost node
row = np.zeros(4*(n-1))
row[:4] = np.array([6*x[0], 2, 0, 0])
matrix.append(row)
target.append(0)
# the rightmost node
row = np.zeros(4*(n-1))
row[-4:] = np.array([6*x[-1], 2, 0, 0])
matrix.append(row)
target.append(0)

# Cook martix and target
matrix = np.stack(matrix)
target = np.array(target)

# (5) Solve the equations
inverse_matrix = np.linalg.inv(matrix)
abcd = np.dot(inverse_matrix, target)

# Define spline function
def spline(x, a, b, c, d):
    return a*x**3 + b*x**2 + c*x + d

# (6) Interplation
x_fine = np.linspace(0, 10, 1000)  # fine grids
y_fine = []
ci = 0  # curve i
for x_i in x_fine:
    if x_i > x[ci+1] and ci < (n-1):
        ci += 1
    a, b, c, d = abcd[4*ci:4*ci+4]
    y_fine.append(spline(x_i, a, b, c, d))

# Plot
plt.figure(dpi=100)
plt.plot(x, y, 'ko')
plt.plot(x_fine, y_fine, 'r-')
plt.show()

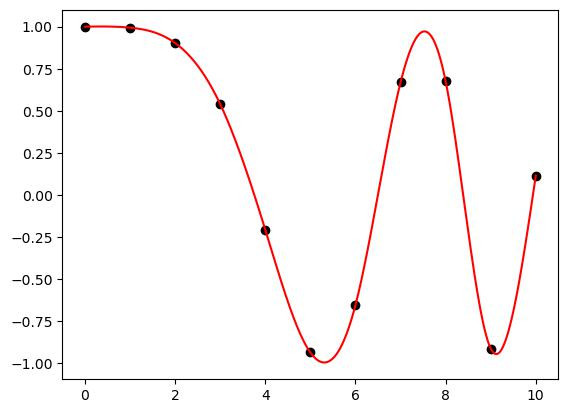
最後插分的部分提供了一個比較naive但直覺的寫法。因為效能的關係，最好盡量使用Numpy做操作。

Scipy演示

如前面所介紹的，Scipy的scipy.interpolate.CubicSpline提供了三次內插，而其中bc_type引數可以指定使用什麼樣的邊界條件。

from scipy.interpolate import CubicSpline
import matplotlib.pyplot as plt
import numpy as np


x = np.linspace(0, 10, 11)
y = np.cos(-x**2/9.0)
y[-1] = y[0]  # make the sequence periodic
x_fine = np.linspace(0, 10, 1000)
bc_types = ['not-a-knot', 'periodic', 'clamped', 'natural']

for s in bc_types:
    f = CubicSpline(x, y, bc_type=s)
    plt.plot(x_fine, f(x_fine), '-', alpha=0.8, label=s)

plt.plot(x, y, 'ko')
plt.grid(linestyle='--', alpha=0.3)
plt.legend()
plt.show()

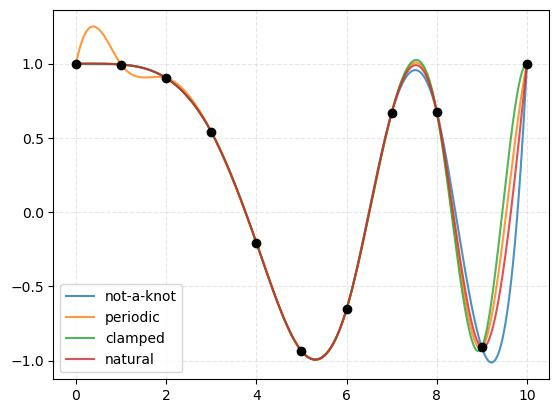
• not-a-knot: 最後與倒數第二條線段為相同線段，如此一來就少了4個方程式條件要滿足。雖然API文件推薦這個模式，但筆者覺得容易造成尾端有過擬合現象。
• periodic: 在兩末端相同的時使用，如此第一與最後一點也可以加入一階與二階導數條件。正如其名，推薦在已知資料點是有週期性的時候再使用。
• clamped: 兩末端點的一階微分為0，可以理解為讓曲線的末端點與水平線相切。
• natural: 兩末端點的二階微分為0，可以理解為讓曲線接近末端點的部分趨近直線。

參考

Lagrange Polynomial Interpolation
scipy.interpolate.CubicSpline
Legacy interface for 1-D interpolation (interp1d)
插值-样条插值