前言

這次會先來介紹XOR跟一些它的特性，之後再來解題!

XOR

• 經典文氏圖!
  

只是覺得南瓜很可愛就想放一下XD

• 為位元運算(把數字換二進位再去做xor)
• 位元運算子 : “ ^ “，數學符號 : ⊕，e.g. a^b 、 a⊕b
• 在條件A 及 B 2項都成立或2項都不成立時 = > 回傳False
• 在條件A 及 B 中有一項成立及另一項不成立 = > 回傳True
• 得出真值表
  

特性

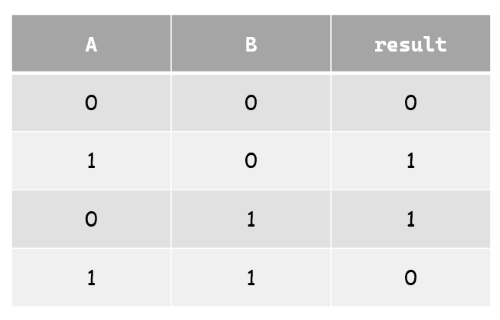
由以上可知

• 當A = B，A⊕B都會為0，所以得出
  • A⊕B = 0、A⊕A = 0 => 相同數字去做XOR會互相抵消為0
• 如B = 0且A != 0， 那麼A⊕B = A，所以得出
  • A⊕0 = A => 任何數字⊕0結果都會為那個數字
• 如A = 1、B = 0，A⊕B跟B⊕A的結果相同(都為1)，所以得出
  • A⊕B = B⊕A => XOR符合交換律

有交換律，感覺少了一點什麼，沒錯!XOR也符合結合律喔!不過要稍微想一下，我們回到真值表(懶得往上滑，所以我再放一次圖( •̀ ω •́ )✧)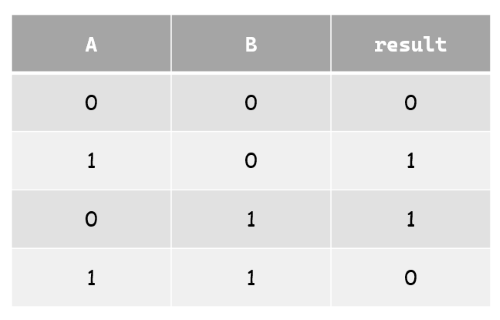

根據result可知，如果A + B為偶數(0、2)那麼結果為0，
反之，如果為奇數(1)那麼結果就為1
所以我們可以設一個函式Odd()，如A+B為奇數，那麼Odd(A+B)就會回傳奇數(1)，
反之為偶數的話回傳偶數(0)，代表我們可以把A⊕B寫成

• A⊕B = Odd(A+B)

有了這個，我們來開始證明結合律!

• 目標 : 證明 A⊕(B⊕C) = (A⊕B)⊕C

A⊕(B⊕C)
=A⊕(Odd(B+C))
=Odd(A+(Odd(B+C))

Odd(A+(Odd(B+C))意思是先把B跟C相加之後判斷奇偶，
如相加為奇回傳奇(1)，
相加偶回傳偶(0)，
之後再加A去判斷奇偶。
所以裡面Odd(B+C)也可以寫成B+C(因為B+C跟Odd(B+C)結果的奇偶性會是一樣的，
比如說B+C是偶數，代表Odd(B+C)會回傳偶，所以兩者結果都是偶數)，
由此可得Odd(A+B+C)

=Odd(A+B+C)
=Odd(Odd(A+B)+C)
=(A⊕B)⊕C

• 由以上可得知，A⊕(B⊕C) = (A⊕B)⊕C
• XOR符合結合律

https://math.stackexchange.com/questions/293793/prove-xor-is-commutative-and-associative 想要更詳細、或著其他方式證明結合律的話可以看這個網址，主要是我被這個證明方式說服了，加上自己對於這種AND OR運算還不是很熟悉，所以就只介紹這個證明方式

特性小整理

符合以下

• A⊕0 = A(恆等律)
• A⊕A = 0(自我抵銷、歸零律)
• A⊕B = B⊕A(交換律)
• A⊕(B⊕C) = (A⊕B)⊕C(結合律)
• A⊕B⊕B = A⊕0 = A(自反)

實作XOR

懂了XOR的特性以及觀念，我們先自己手算xor一次，之後再用code來驗證、實作一次吧!

先來隨便設兩個變數，A = 97、B = 15

• 目標 : 輸出A XOR B的結果

• 流程 : 先把A跟B轉為2進位，之後一個一個bit做xor，最後把結果轉回10進位得出答案

• 先來把兩數轉二進位
  使用短除法，得到餘數之後由下到上就是該數的二進位!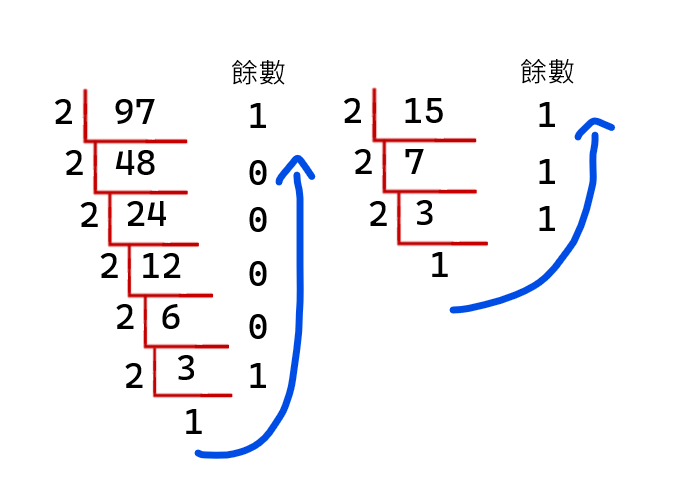
  

• 得 A = 1100001、B=1111，接下來做XOR

之後要一個一個做XOR的時候會發現一個大問題，那就是兩個長度不同!
解決方法為在比較短的左側去補零，我們上圖!紅色的0就是補0的部分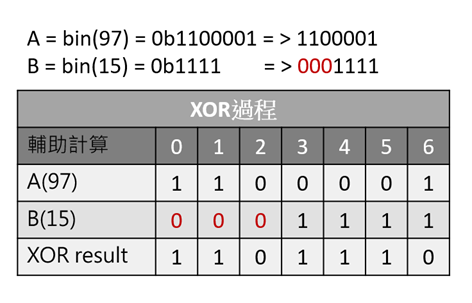

而為甚麼在左側補0不會影響結果，我們放到最後再來!可以想想看XD

接下來要把結果換成10進位。如XOR result為1，就把它對應的2的次方取出來，結果為 110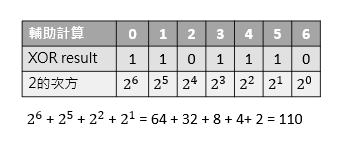

手算完後，我們用程式碼來進行驗證，有兩種方式，第一個為使用^來做XOR，第二種為使用pwntools函式庫中的xor()

所以使用時要記得from pwn import *

• Code

from pwn import *
num1 = 97
num2 = 15

print("use ^ :", num1^num2)
print("use xor :", ord(xor(num1,num2)))

• Output
  

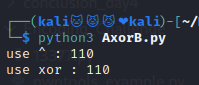
可知兩種方式結果都是一樣的(不過使用xor()他出來會直接轉成字符，所以我偷偷用了ord()把它變回數字)，與我們手算的結果也相同!皆大歡喜R (°▽°)╯

小結

終於結束惹，OMG，位元運算的部分，對於我來說，理解有一點小小吃力，尤其是證明的時候(┬┬﹏┬┬)不過最後弄懂，也學到了好多咚咚
不過還沒完!還記得在實作XOR問的問題嗎，我們再來理解一下吧XD

為甚麼在左側補0不會影響結果

可以參考這張圖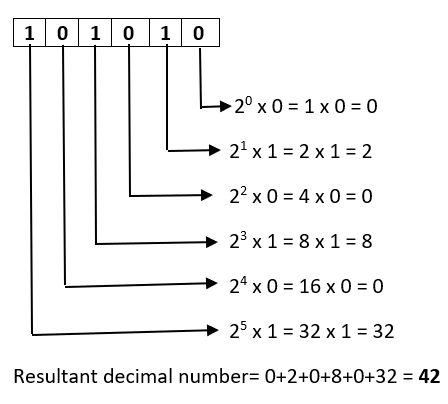

由此可知，當二進位值為0的話，不管位於哪，乘出來的結果都會是0，所以可推得
int(101010,2) = int(00101010,2)
一樣用圖表顯示

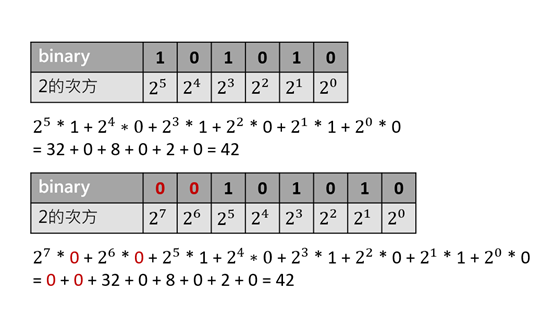
下面為在左側加兩個0，但會發現，因為是乘0的關係，所以最後加起來的值是一樣的。

• 推得，左側加0並不會影響最後結果!

理解完畢!今天大概就到這裡惹，休息!明天開始正式解題~

參考資料

XOR維基百科: https://zh.wikipedia.org/zh-tw/%E9%80%BB%E8%BE%91%E5%BC%82%E6%88%96

XOR文式圖 : https://www.cool3c.com/article/157771

XOR位元運算子介紹 : https://medium.com/@hyWang/xor-%E4%BD%8D%E5%85%83%E9%81%8B%E7%AE%97%E5%AD%90-1c25b4ae15fb

證明XOR結合律(Prove XOR is commutative and associative) : https://math.stackexchange.com/questions/293793/prove-xor-is-commutative-and-associative

兩數二進位長度不同做XOR : https://stackoverflow.com/questions/31520787/how-to-xor-two-binary-numbers-having-different-length

二進位算法 : https://tomchun.tw/tomchun/2015/11/11/1-91/

二進位轉十進位 : https://www.geeksforgeeks.org/binary-to-decimal/