昨天講了對稱加密的串流加密法，今天來談對稱加密的分組加密技術

分組加密是將明文分割成固定大小的組，將這些固定大小的組送進特殊數中生成固定大小的密文

同樣地，假設明文P會先以眾所週知的轉換方式以二進位數表示

我們先從一個簡單的例子出發，從中認識分組加密的一些特徵：

費斯妥密碼

明文P會先被分成左半與右半

接著進行第一回合，我們讓新的左半邊等於舊的右半邊 ，而新的右半
其中 是昨天學過的XOR運算， 是根據密鑰K得到的，屬於第一回合的子密鑰
將子密鑰與上一輪的右半邊一起從到函數F當中，吐出來的東西與上一輪的左半邊XOR一次得到新的右半邊

第二回合的操作也是：,
同樣的步驟持續遞迴運算，到第n輪，可以得到
,

持續進行同樣的步驟，到第n步時，得到最終密文

其圖解如下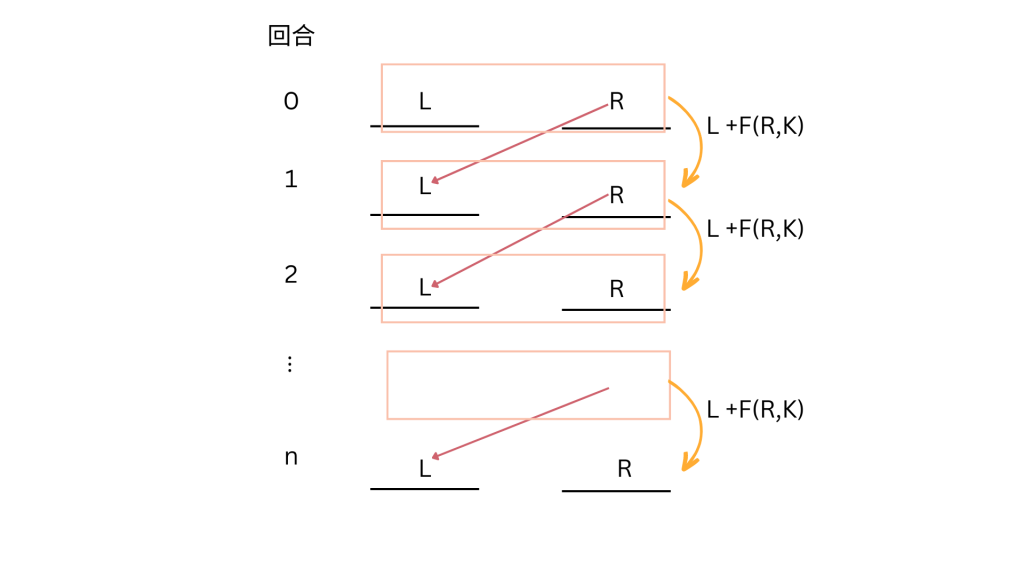

由於函數F被不斷的遞迴使用，因此他又被稱為回合函數(round function)，而重複的次數n，則稱為分組加密的回合(rounds)
使用遞迴是分組加密技術的一項特點

想要解碼費斯妥密碼，只需要將步驟倒過來即可(利用XOR兩次回到自身的原理)

假如手上有第n輪的結果，第n-1的結果即為

不斷重複動作

可得到原始明文P

任何的函數F，只要其輸出的長度符合規定，都可以讓費斯妥密碼成功運行，舉例來說，一個最無聊的F

總是輸出0，也是可以成功加密，不過會發現其結果跟沒有加密一樣

其他分組加密

我們可以由以上例子看出，選擇一個好的回合函數以及生成子密鑰的過程會是分組加密法的關鍵
比較著名的分組加密演算法DES便是在回合函數F與生成子密鑰的方式增加許多機關，讓破解的方法變困難
不過DES的演算法特性，只能接受56位元的密鑰K，過小的密鑰空間讓這個演算法逐漸被淘汰

後續研發出的AES可以接受到256位元的密鑰，讓整個演算法更加安全
雖然同樣也是分組加密技術，不過他不是用費斯妥密碼的方式加密，而是仰賴更加複雜的數學結構

其他著名的分組加密有IDEA, Blowfish, RC6, TEA
雖然基本結構都不是用費斯妥加密，不過概念上仍是將明文一塊一塊地加密，而非以一個位元為單位的方式加密

小結

今天我們介紹分組加密中的基本費斯妥加密
以及列出其他分組加密的技術
其他超出費斯妥加密技術的東西，以及分組加密的其他分組技術以及加密模式有礙於時間關係只好跳過

為了介紹之後更加有趣的章節，明天得來上個數學課