對稱加密要求加密和解密的兩端持有相同的密鑰
對稱加密最大的困擾就是，該如何安全地讓大家都知道加密者的密鑰
昨天也談到可以用DH的方法安全地讓大家拿到相同的密鑰

公鑰加密方法則是採用另種手法解決了這個問題

每個人可以有兩種不同的鑰匙
一把鑰匙是可以公開地揭露，稱作公鑰
另一把則是私下保存的私鑰

假設Bob擁有公鑰和對應的私鑰，任何人都可以將明文用公鑰加密傳輸給Bob，只有Bob可以用他的私鑰將該段密文解密

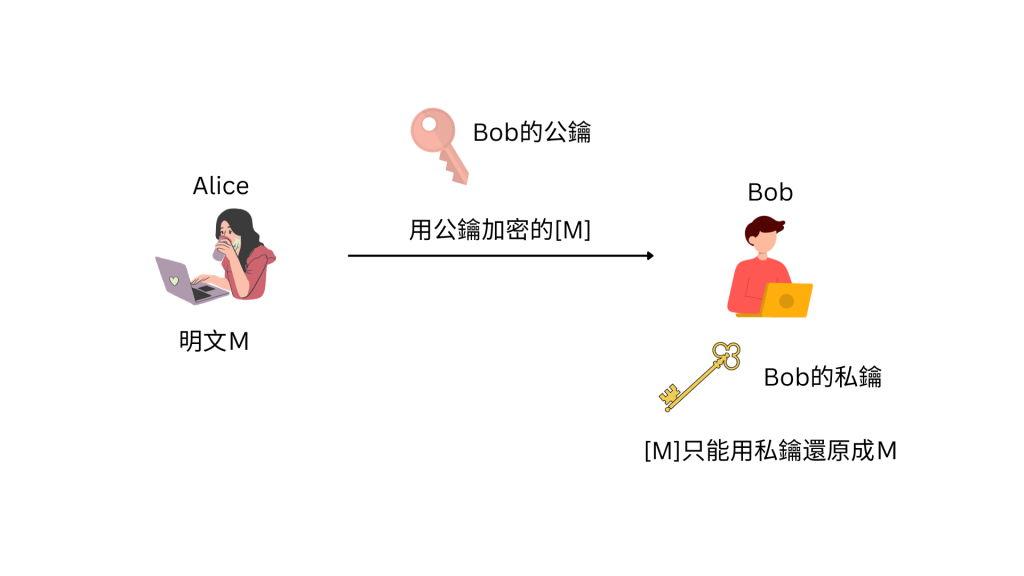
不只這樣，反過來Bob可以用他的私鑰對一段文字進行加密，大家可以利用公鑰將該段文字解密，
由於只有Bob擁有的私鑰可以辦到讓公鑰能夠解鎖，如此反向操作便可實現電子簽章的效果，證明該段文字確實由Bob所加密簽署

話說如此，相較於大量的對稱加密系統，目前已知可用的公鑰加密系統數量相當稀少
主要原因是其背後的支持的數學系統相當複雜，讓他在研發的過程相當困難

接下來要講的背包加密法(knapsack)算是最早被研發出的公鑰加密技術，他利用演算法問題中NP完備的性質來做設計
因此我們今天先岔題一下，了解NP完備的問題是什麼意思

簡介P, NP, NP完備問題

這邊介紹在演算法中經常用到的觀念

在電腦科學中，有一些問題，我們找到能夠在多項式的時間之內被解出的方法

也就是說我們可以事先找到一個數字k
可以預測輸入值的大小b的東西，其所需計算時間上限不超過

這些問題被稱作P問題，著名的例子有

• 排序
• 線性規劃
• 檢查一個數字是否為質數

而有另一群問題，要檢查答案是否正確只需花多項式時間
就像數獨一樣，要檢查一個數獨結果是否滿足要求很容易就可以完成

這種檢查答案很簡單的問題稱作NP問題

整數分解也是個著名的NP問題，要檢查兩個因數相乘起來是否為給定的整數是相當簡單的

由於每個P問題都能夠在多項式時間之內被解出，要檢查答案自然也能夠在多項式時間之內完成，因此所有P問題都是NP問題

而NP問題中最 困難 的問題，我們稱為NP完備問題，著名的NP完備問題有：

• 給定一張圖，是否存在比某個數n還要大的最短路徑
• 給定一張圖，是否存在一條路徑可以不重複地經過所有節點
• 給定一個有限集合X和包含一些X子集的集合F，能否在F中選出不大於某個數字k的集合們覆蓋X

比較有趣的是，一些長輩們在玩的Candy Crush 也是NP完備問題

這些NP完備問題有個有趣的特點，一但某個NP完備問題的多項式演算法被找到，其他的NP完備問題也可以用同樣的演算法，在多項式時間內被解開

不過至今為止，該演算法始終沒能被找到，也無法證明該演算法不存在，
若能夠找到該演算法，就意味著所有NP問題都有一個多項式演算法可以解出，因此就可以證明出 ；反之若能證明該演算法不存在，即證明出

了解一個問題是不是NP完備相當重要，由於P是否等於NP是數學界有名的七大千禧年大獎難題之一，因此一但意識到這個問題是NP完備，除非你夠厲害，否則放棄找尋最佳的演算法的時間會是比較明智的抉擇，畢竟全世界的天才都找不到了，我們大可將精力投注於其他更有效率的事情