在進行對稱加密時,一個很大的困難就是如何秘密地分享對稱密鑰
今天要來介紹的主題就是探討這個問題
Diffie-Hellman演算法(DH),是讓兩端用戶互相安全地交換密鑰的方法
用到的是取log很困難這件事來做設計
給定正數g和x,想要計算怎樣的k,可以滿足
我們可以藉由計算 得到
在離散的版本,g和x都是比p(質數)小的正整數,我們想問怎樣的k可以滿足
因為兩者形式很相近,因此又稱為離散對數問題
離散對數與質因數分解一樣都是NP問題(之後會再詳細介紹)
兩者都是出了名的困難,至今為止無法找到多項式時間可以完成的演算法
有幾件事必須先說明:
由於p故意選質數,根據某些有趣的性質, 每個數字除以p的餘數都會不一樣
因此k一定能在1~p之間被找到
我一開始看到這邊會有些疑惑,畢竟最多只要嘗試p次就可以找到k,為什麼會說這個問題很困難呢?
要注意這邊的多項式時間是以p的位元做計算,舉例來說p若以b位元表示(可以是 以下的質數,用0和1表示) 那麼以上從k=1慢慢找,找到
會是以b的指數作增長
也就是說我只要再多一個位元表示p,所需花的努力就是2倍
要是以足夠多的位元表示足夠大的p,那麼用一個一個慢慢找的方式來解k幾乎是不可能的
p會選擇一個質數並公開
g選擇一個比p小的正整數也公開
實際密鑰交換的情況如下:
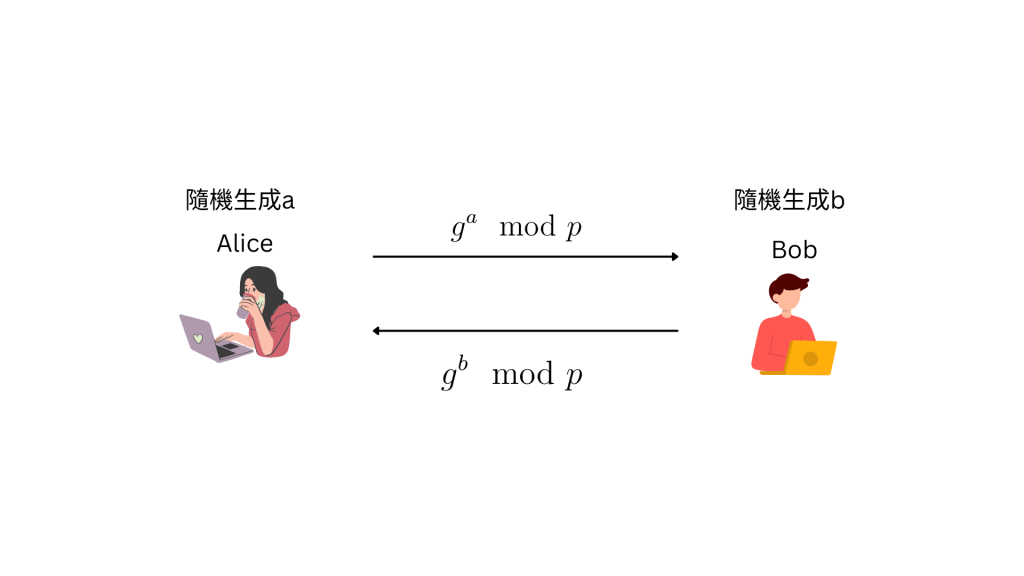
從中攔截的Trudy只能看到 與
,想要得到
勢必得解出a或b才行
由於解a, b需要取離散對數,Trudy無法從中提取任何密鑰的資訊
取p=5231,Alice隨機生成a=4579, Bob隨機生成b=3558
兩人共同協議取g=2178
Alice計算 傳送給Bob
Bob計算 傳送給Alice
從Alice那端攔截到4162的Trudy必須解很難的離散對數才能得出4579;從Bob那端攔截到4614的Trudy必須解很難的離散對數才能得出3558
Alice收到4614後,取a次方可得; Bob收到4162後取b次方可得
458即為兩人分享的密鑰
其python計算如下:
import numpy as np
p = 5231
g = 2178
np.random.seed(12345)
a = np.random.randint(1, p)
b = np.random.randint(1, p)
ga = pow(g, a, p)
gb = pow(g, b, p)
print(ga)
print(gb)
gab_Alice = pow(gb, a, p)
gab_Bob = pow(ga, b, p)
print(gab_Alice)
print(gab_Bob)
這邊先給各位一點過很多天才會談到的認證問題的動機
DH演算法容易受到中間人攻擊(man-in-the-middle)
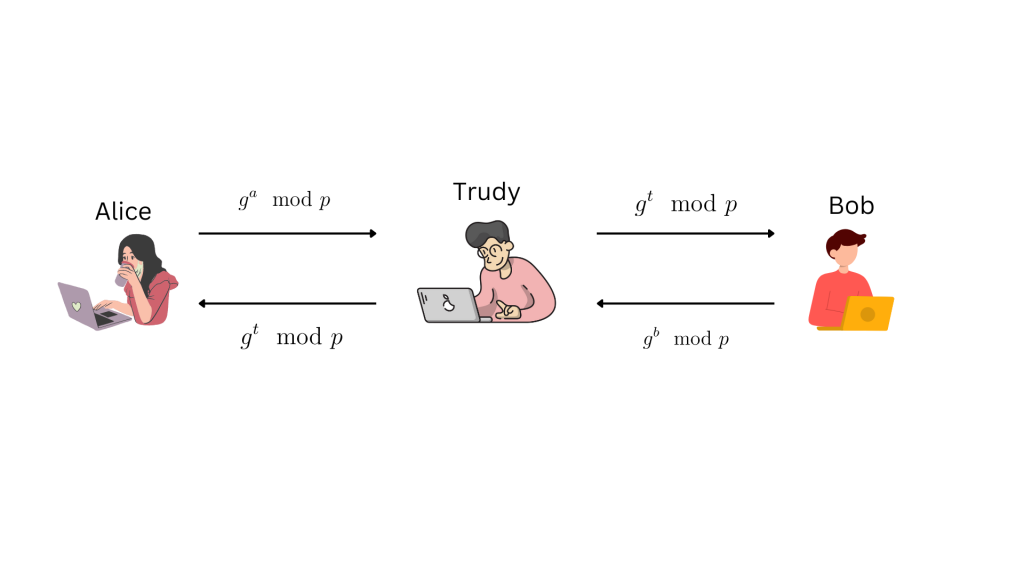
Trudy可以主動地於中間攔截Alice送過來的訊息,假裝自己是Bob回傳給她,跟Alice建立起 的共同密鑰;
Trudy也可以假裝自己是Alice攔截Bob的訊息,並回傳訊息,與Bob建立 的共同密鑰
中間人問題的發生就是因為參與的雙方沒有經過 認證(Authenticated)
不能確定自己在跟誰溝通,因此容易發生資安的危險
