今天我們會介紹擴散模型 (Denoising Diffusion Probabilistic Model,DDPM) 相關的內容,包含:擴散 (Diffusion)、去噪 (Denoise)、演算法、近期回顧、及補充。
擴散的過程是前向過程 (forward process),它會將雜訊加入至原先的圖片當中,直到無法辨識原圖片為止,其中的雜訊是高斯分佈的,也就是常態分佈的雜訊,使用常態分佈的好處是容易理解,整體流程如下圖所示。
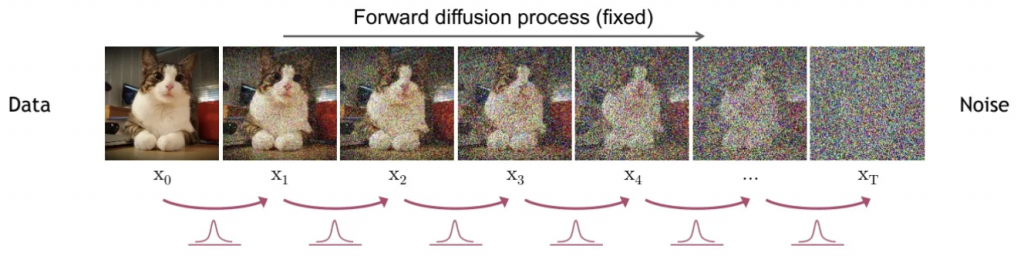
可以看到貓的圖片經過加入高斯雜訊的流程,圖像逐步添加了雜訊,直到看不清原圖為止,這個圖像就是隨機雜訊的圖像。
去躁的過程是反向過程 ( reverse process ),它會將隨機雜訊的圖像,逐步還原回原始的圖像,整體流程如下圖所示。

可以看到隨機雜訊的圖像,經過層層的去除雜訊處理處理後,會還原成原本的圖像,這就是去躁的學習過程。
這一小節我們深入探討一下其中的演算法,主要分為訓練、生成兩個部分。

具體來說,原理上在擴散的過程中,實際上是用到了去躁步驟的反向邏輯,那麼是如何做到這點的?我們可以回顧下以前在去躁的做法,一般來說就是使用去躁的自編碼器 (Denoise Auto-encoder, DAE),在這邊除了原始作法的DAE外,還加上了Score Matching及Langevin dynamics的方法。
Score Matching是一種參數估計的方法,相較於傳統的蒙地卡羅方法 (Markov Chain Monte Carlo method, MCMC) 較為節省時間,原因是它可以透過複雜函數中的導數去做估計。
Langevin dynamics是來自於分子動力學的方法,在這邊主要是為了要找到要訓練的目標函數,這個目標函數不是一蹴可幾的,它只有紀錄倆倆狀態之間的關係,讓每一次的變化幅度都相同。
因此,訓練階段,主要是透過目標函數去訓練生成雜訊的模型,而在生成階段,主要是從高斯分佈的雜訊中,用模型生成的雜訊,逐步分離訊號,直到獲得我們所要的生成數據為止。
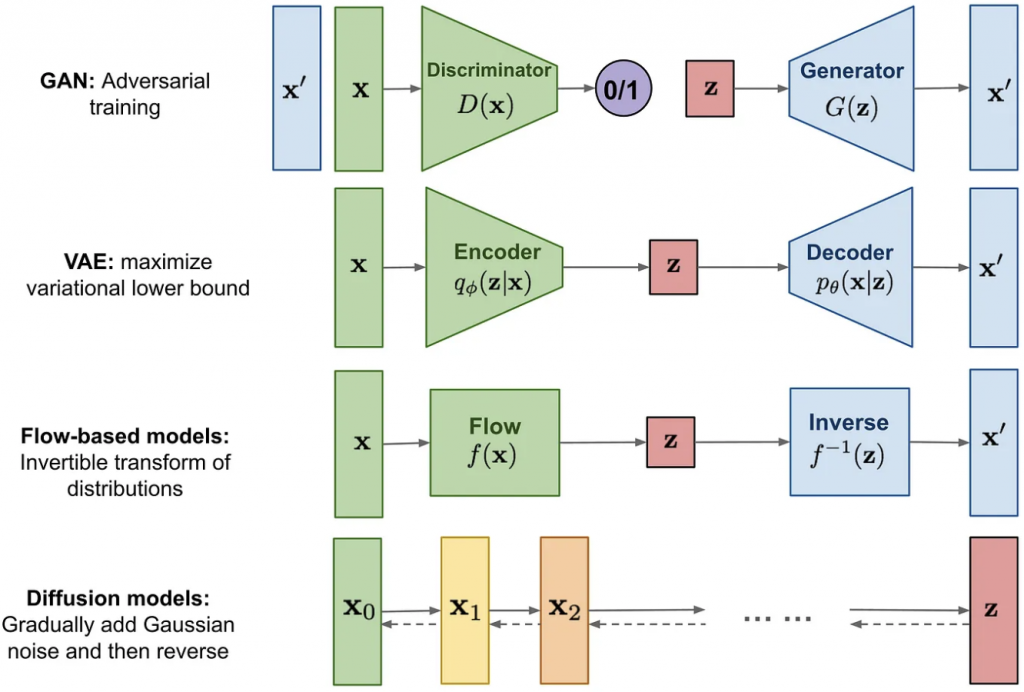
在這我們簡單回顧一下介紹過的模型;例如,GAN、VAE、Flow-based models、Diffusion models,可以看到他們都是分為兩個組件的架構,而這兩個組件是互為逆反的。

今天我們介紹了主軸中的Diffusion Model,其中的關鍵是,學習相鄰兩狀態的關係,找到其目標函數,計算出差異的雜訊,作為添加隨機的反向雜訊的依據,進而生成我們要的數據,後續,我們會接續討論其他的相關方法,明天見!
