補一下前幾天的演算法類型 ~

Single Source Shortest Paths

Single Source Shortest Paths 是圖論和計算機科學中的一個重要問題，通常用於尋找兩個點之間的最短路徑或最短距離。

這個問題在許多領域都有廣泛的應用，包括交通規劃、網絡路由、物流和路徑規劃等。

最著名的最短路徑演算法包括：

1. Dijkstra's Algorithm：用於找到單源最短路徑，即從一個起始點到圖中所有其他點的最短路徑。該演算法法使用貪婪策略，逐步選擇距離起始點最近的點，然後更新到其他點的距離。
2. Bellman-Ford Algorithm：用於找到單源最短路徑，與 Dijkstra 演算法不同，它可以處理包含負權邊的圖。然而，它的時間複雜度較高，通常在沒有負權回路的情況下使用。
3. Floyd-Warshall Algorithm：用於找到圖中所有點對之間的最短路徑。該演算法通過動態規劃的方法計算任意兩點之間的最短路徑，適用於有向圖和帶權圖。

這些演算法的選擇取決於具體的問題和圖的性質。

最短路徑問題是計算機科學中的經典問題之一，透過改進演算法以提高效率和適用性。

今天要來介紹的演算法是 Minimum spanning tree

Minimum spanning tree

Minimum Spanning Tree (MST）是圖論和計算機科學中的一個基本概念。

它是一個連通的無向圖的邊的子集，連接了所有的頂點，並且具有可能的最小總邊權重。

最小生成樹的關鍵特性包括：

1. 連通性：一個MST確保圖中的所有頂點都是連通的。這意味著你可以通過沿著樹的邊從任意兩個頂點之間移動。
2. 無環：最小生成樹不得包含任何循環。向樹中添加一條會形成循環的邊會使其成為一個生成子圖，但不是樹。
3. 最小權重：最小生成樹的權重（或成本）是所有可能的生成樹中最小的。生成樹的權重是其邊的權重（或成本）之和。

最小生成樹在不同領域中有不同的應用，包括網絡設計、集群分析和優化問題的近似算法。

Prim's Algorithm

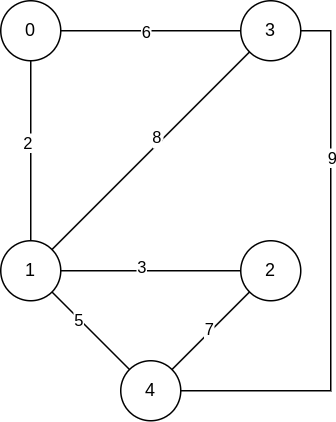
從一個任意的起始頂點開始，然後重複添加連接最小權重的邊，這些邊連接了 MST 中的一個頂點與 MST 外的一個頂點，直到所有頂點都包括在 MST 中。

// Prim's algorithm in Kotlin

import java.util.PriorityQueue

// Edge class
data class Edge(val from: Int, val to: Int, val weight: Int)

// Graph class
class Graph(val vertices: Int) {
    val nodes = IntArray(vertices)
    val edges = mutableListOf<Edge>()

    fun addEdge(from: Int, to: Int, weight: Int) {
        nodes[from] = from
        nodes[to] = to
        edges.add(Edge(from, to, weight))
    }
}

class Prim(val graph: Graph) {
    val mst = mutableListOf<Edge>()
    val visited = mutableSetOf<Int>()
    val pq = PriorityQueue<Edge>(graph.edges.size, compareBy { it.weight })

    fun run() {
        val start = graph.nodes[0]
        visited.add(start)
        addEdges(start)
        while (pq.isNotEmpty()) {
            val edge = pq.poll()
            if (edge.to !in visited) {
                mst.add(edge)
                visited.add(edge.to)
                addEdges(edge.to)
            }
        }
    }

    fun addEdges(node: Int) {
        for (edge in graph.edges) {
            if (edge.from == node && edge.to !in visited) {
                pq.add(edge)
            }
        }
    }
}

// main function
fun main(args: Array<String>) {
    val graph = Graph(5)
    graph.addEdge(0, 1, 2)
    graph.addEdge(0, 3, 6)
    graph.addEdge(1, 2, 3)
    graph.addEdge(1, 3, 8)
    graph.addEdge(1, 4, 5)
    graph.addEdge(2, 4, 7)
    graph.addEdge(3, 4, 9)
    val prim = Prim(graph)
    prim.run()
    println("Minimum Spanning Tree:")
    for (edge in prim.mst) {
        println("${edge.from} -> ${edge.to} = ${edge.weight}")
    }
}

Kruskal's Algorithm

從一個空的邊集合開始，然後迭代地添加最輕的邊（權重最小的邊），這些邊不會在當前邊集合中形成循環，直到所有頂點都連接在一起。

由 Schulllz - 自己的作品, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=30888975

// Kruskal's algorithm in Kotlin

import java.util.PriorityQueue

// Edge class
data class Edge(val from: Int, val to: Int, val weight: Int)

// Graph class
class Graph(val vertices: Int) {
    val nodes = IntArray(vertices)
    val edges = mutableListOf<Edge>()

    fun addEdge(from: Int, to: Int, weight: Int) {
        nodes[from] = from
        nodes[to] = to
        edges.add(Edge(from, to, weight))
    }
}

// Union-Find class
class UnionFind(val size: Int) {
    val parent = IntArray(size)
    val rank = IntArray(size)

    init {
        for (i in 0 until size) {
            parent[i] = i
        }
    }

    fun find(x: Int): Int {
        if (parent[x] != x) {
            parent[x] = find(parent[x])
        }
        return parent[x]
    }

    fun union(x: Int, y: Int) {
        val rootX = find(x)
        val rootY = find(y)
        if (rootX == rootY) return
        if (rank[rootX] < rank[rootY]) {
            parent[rootX] = rootY
        } else if (rank[rootX] > rank[rootY]) {
            parent[rootY] = rootX
        } else {
            parent[rootY] = rootX
            rank[rootX]++
        }
    }

    fun connected(x: Int, y: Int): Boolean {
        return find(x) == find(y)
    }
}

class Kruskal(val graph: Graph) {
    val mst = mutableListOf<Edge>()
    val uf = UnionFind(graph.vertices)
    val pq = PriorityQueue<Edge>(graph.edges.size, compareBy { it.weight })

    fun run() {
        for (edge in graph.edges) {
            pq.add(edge)
        }
        while (pq.isNotEmpty()) {
            val edge = pq.poll()
            if (!uf.connected(edge.from, edge.to)) {
                uf.union(edge.from, edge.to)
                mst.add(edge)
            }
        }
    }
}

// main function
fun main(args: Array<String>) {
    val graph = Graph(5)
    graph.addEdge(0, 1, 2)
    graph.addEdge(0, 3, 6)
    graph.addEdge(1, 2, 3)
    graph.addEdge(1, 3, 8)
    graph.addEdge(1, 4, 5)
    graph.addEdge(2, 4, 7)
    graph.addEdge(3, 4, 9)
    val kruskal = Kruskal(graph)
    kruskal.run()
    println("Minimum Spanning Tree:")
    for (edge in kruskal.mst) {
        println("${edge.from} -> ${edge.to} = ${edge.weight}")
    }
}

除了以上兩種演算法之外

Boruvka's Algorithm：將圖分成多個子圖，然後在每個子圖中找到最小生成樹，最後將這些最小生成樹合併成一個更大的生成樹。

所有 Code 可以在 Github 找到 ～

明天將進入新的主題 Dynamic Programming

Reference

• 普林演算法
• 克魯斯克爾演算法