IndexType: GiST

前言

前面章節介紹了BRIN可以存一個可比較的範圍，
那如果今天想搜尋笛卡爾坐標系呢?
這時候就是我們GIST出場的時候了!

R Tree

在介紹GIST前，必須先了解一下R Tree
R Tree是一個專門存取座標點的結構的平衡樹。
R Tree的「R」代表「Rectangle（矩形）」，
可以想像一下B Tree是拿來做一維存取，
而R Tree是拿來做二維三維等更高維度的存取，
leaf node為座標點，
中間的internel node也是非常有意義的。
他可以代表一個一個的矩形被所框住的點。

當插入一些點時，R Tree就如同B Tree，會分裂出子點
就如同下圖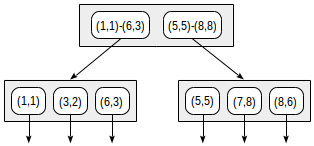

create table points(p point);

insert into points(p) values
  (point '(1，1)')， (point '(3，2)')， (point '(6，3)')，
  (point '(5，5)')， (point '(7，8)')， (point '(8，6)');

我們來觀察一下中間的internel node，
可以發現他剛剛好就是一個矩形，像第一個internel node
(1，1)-(6，3)，在坐標系中剛好框出一個矩形，如下圖

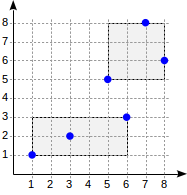
當有很多點時就會一層一層的疊加上去，如同下圖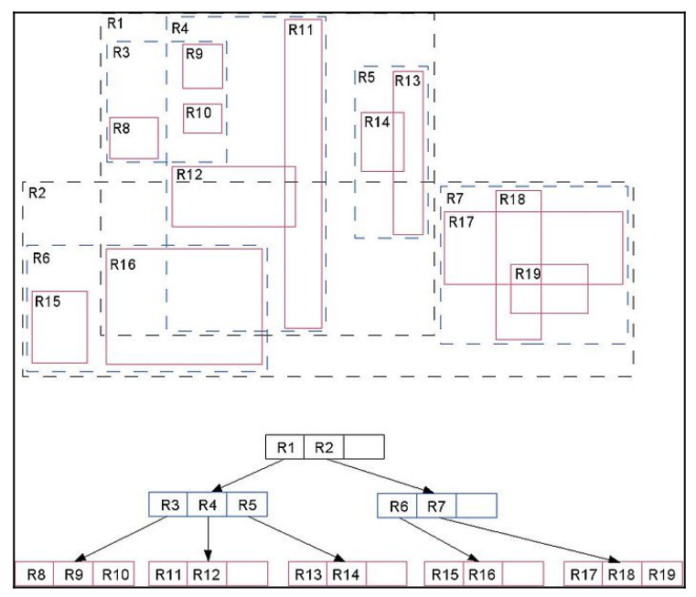

這剛剛好就符合了地圖搜尋的特性

GiST

終於介紹到今天的主角了，GiST(Generalized Search Tree)通用搜索树。
GiST事實上並不是一個資料結構，他是一個樹狀結構搜尋的方法。
像是我們在B+Tree內在搜尋時，會使用<， > ，=等符號來搜尋，
但是今天要搜尋R Tree時，他就使用了許多的矩形來建立tree，如果今天要搜尋的範圍可能跨多個矩形，總不可能直接無腦的將所有點都確認一次，
我們可以透過GiST這個搜尋方法，先在internel node做範圍的確定，然後再經過一層一層的比對，最後選中我們目標的那些矩形，最後輸出結果。

因此，透過R Tree來建立index結構，然後透過GiST協助搜尋R Tree，提供接口，大幅了降低R Tree尋找的難度。

使用場景

1. 笛卡爾坐標系
2. 多維度資料
3. 城市行政區
4. 地圖

使用GiST

建立point

insert into points(p) values (point '(1,1)');

建立index

create index on points using gist(p);

搜尋

select * from points where p <@ box '(2,1),(7,4)'
<@代表包含的意思
box'(2,1),(7,4)' 是我們劃出的矩形

explain select * from points where p <@ box '(2,1),(7,4)';

                  QUERY PLAN                  
----------------------------------------------
 Index Only Scan using points_p_idx on points
   Index Cond: (p <@ '(7,4),(2,1)'::box)
(2 rows)

結語

這個章節，我們可以輕易的了解R Tree協助分點分群特性，
並且使用GiST來協助R Tree的搜尋。
以後如果需要做與地圖或笛卡爾坐標系等應用時，
千萬要記得使用喔，否則你的搜尋一定是全表搜尋，效能會非常的慘。

參考資料

1. R樹
2. Indexes in PostgreSQL — 5 (GiST)
3. GiST
4. Chapter 49. GiST Indexes