目的

傅立葉轉換，可以用很多種方式來詮釋它，從直觀上理解傅立葉轉換，可以想成信號是無限個不同頻率的餘弦波跟正弦波組成。傅立葉轉換可以幫助我們找到信號的主要頻率，進而忽略雜訊。

從數學的角度上來看，傅立葉轉換可以被視為多項式乘法。為什麼信號可以用多項式表示呢？以一次多項式來看，所有 x 的點集合會形成一條直線；二次多項式則是曲線，以此類推。在這類型的應用中，我們通常不是為了要求出 x 的解，而是想要對波形做計算。

例如低通濾波、高斯模糊等等，這些計算本質上是對兩個多項式乘法。在計算機領域當中，對信號做計算時採樣通常都會是離散的資料，因此稱作離散傅立葉轉換（DFT）。

直接將兩個多項式展開相乘需要 O(n^2)，對計算來說是我們想要避免的，快速傅立葉轉換可以讓我們在 O(nlogn) 的複雜度做傅立葉轉換。

所謂的轉換是將時域信號轉為頻域。這麼做不是為了好玩，而是轉為頻域後對於分析跟處理有相當大的幫助。

舉例來說，這是一個頻率為 3Hz 的正弦波。 x 為時間（秒）， y 則為振幅（或聲音大小）。

從這張圖表上我們可以得知頻率為 3Hz，因為每秒鐘有三個正弦波週期。 但是真實世界中的頻譜圖會比一個單純的正弦波來得複雜，除非你有絕對音感，不然很難得知當前的頻率為何。

比如說下面這張圖，應該很難用肉眼看出來頻率為何：

另外一個問題則是我們沒辦法對比較複雜的訊號做計算，因為根本不知道這坨複雜的訊號到底要怎麼分析。 然而傅立葉轉換可以讓我們很輕易地將時域轉為頻域。

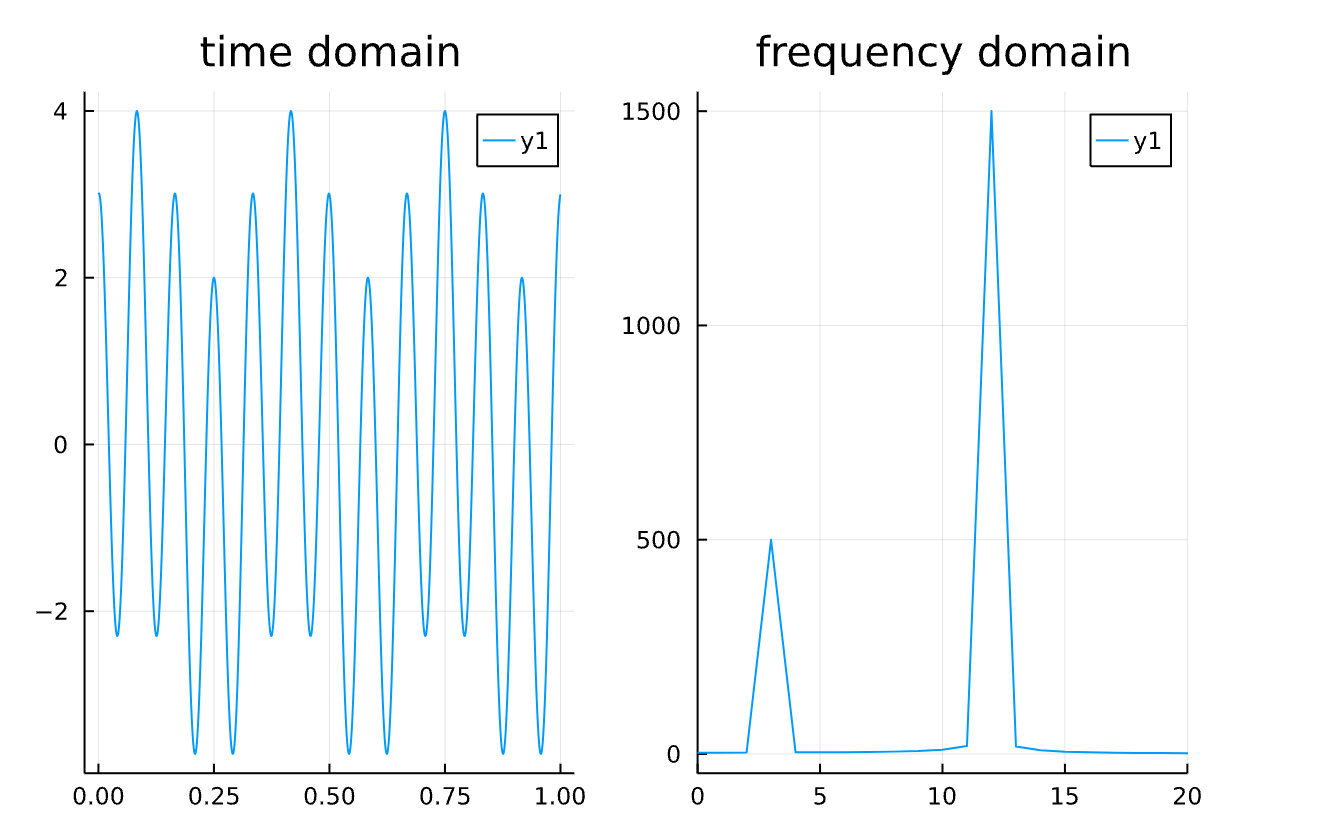
左邊的圖表（時域）經過傅立葉轉換後變成了頻域。可以發現圖中有兩個很明顯的 peak。這代表原始信號當中最重要的頻率是 13Hz + 3Hz 組合而成。

傅立葉轉換不但可以從時域轉為頻域，也可以從頻域轉為時域。

一旦知道傅立葉轉換的精華，整個處理就會變得非常清晰簡單。我們先將時域的信號轉為頻域，在頻域當中做一些處理，然後再轉回去時域信號，雖然變來變去看起來很麻煩，但事實上大大簡化了處理成本。圖片壓縮、mp3、濾波、去雜訊，幾乎現代科技的應用都有傅立葉轉換的影子。

範例：去噪音（denoise）

一個常見的應用是我們希望將噪音去除。這時傅立葉轉換就是一個相當好用的工具。

可以發現在各個頻域當中有很多小波浪，然而我們還是可以很輕易地找到主頻率。

任何理解傅立葉轉換原理的人，應該會對這美妙的定理感到敬畏與感恩，這應該是在工程領域當中最重要的公式之一。原本難以解析的信號透過傅立葉轉換後操作起來如此簡單。