Day8-二元分類

生死關頭

大多數人都經歷過九二一大地震，那場地震造成多人死亡，因此希望能在下一次地震發生時事先預防，透過分類模型來預測誰可能會在地震中喪生。由於分類只有生與死兩個選項，這是一個二元分類問題。

分類問題

分類問題是將樣本分類成有限個數的類別，也就是類別數量通常是有限的，如三個、五個、十個等。當類別數量只有兩個時，即輸出只有兩種情況，這種情況稱為二元分類。經過學習後產生的模型稱為分類器。

二元分類

分類與回歸的區別

分類問題與回歸問題的最大不同在於輸出y的形式。回歸問題的輸出y是一個連續數字，存在著大小的相對關係；而分類問題的輸出是有限數字的集合，各輸出之間沒有大小關係。

二元分類模型

假設有兩個特徵，可以劃出一個特徵空間，使用線性方程式將平面一分為二，該線性方程式可寫為：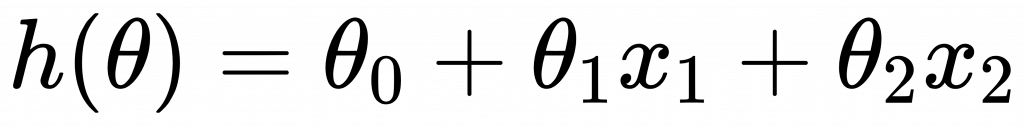

將樣本點代入此方程式可得到輸出值。如果 ( h(x) > 0 )，則預測 ( y = 1 )；若 ( h(x) < 0 )，則預測 ( y = 0 )；若 ( h(x) = 0 )，稱之為決策邊界（Decision Boundary）。此模型與線性回歸模型類似，可以使用梯度下降法來求解，實際上稱為最小平方分類器（Least Square Classifier, LSC）。

LSC的問題

LSC在樣本分布不夠集中的情況下會有偏差。例如下圖中，雖然應該使用綠色線進行分類，但機器學習結果可能會得出橘色線，這是因為LSC會選擇使偏差最小的線。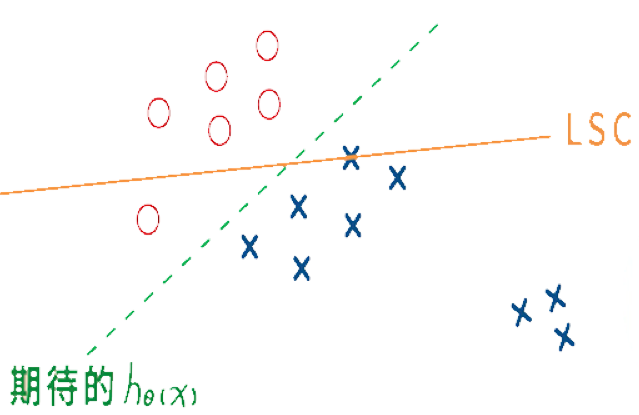

分類問題的誤差計算

與回歸問題不同，分類問題中不關心樣本離決策邊界的距離，只關心樣本是否選對邊。為了壓縮輸出，可以使用數學函式 "1/(1+e^-z)" ，其中 ( z = h(x) )，這個函式稱為S形函數（Sigmoid Function）。經過轉換後，輸出範圍會被壓縮到0與1之間，這表示發生某種情況的可能性。若預測到很大的數字，則 ( y ) 屬於1類；若是負的很大的數字，則表示不像1，這種分類器稱為邏輯斯回歸（Logistic Regression）。若輸出小於0.5則為第1類，反之為第2類。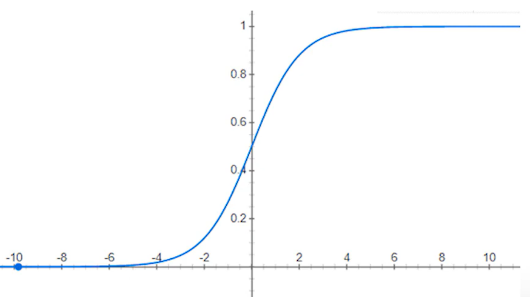

機器學習方法

使用梯度下降法進行學習。前述提到可以使用均方誤差來計算誤差，但因S形函數帶有指數向，較好的方法是取對數，使用以下方法計算誤差：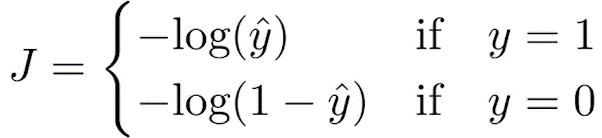

這樣一來，若預測正確，誤差為0；若預測錯誤，誤差接近無限大。