今天延續上一個主題--雙指針，前面僅介紹了雙指針的左右指針，另外一種 -- 快慢指針，今天會搭配Floyd Cycle Detection Algorithm(又稱為龜兔賽跑算法(Tortoise and Hare Algorithm))一起學習，因為在解題的時候發現這兩個演算法其實應該一起學，這樣對於解題的幫助較大!

快慢指針顧名思義，就是在每次移動時，兩指針移動的速度一快一慢，通常會用來處理linked list，以下為常見的應用場景:

1.尋找linked list的中點:
快指針一次移動兩個節點，慢指針一次僅移動一個節點，當快指針抵達尾節點時，慢指針會剛好停在中點
2.尋找linked list的倒數第k個節點(node):
把快慢指針當成一個直尺，先讓快指針走k步，在讓兩指針開始等速前進(保持k距離)，等快指針抵達最後一個節點(node)時，慢指針會停在倒數第k個節點上。

3.判斷linked list是否有cycle
4.尋找linked list的cycle起始點
5.計算linked list的cycle長度

以上3.-5.可以觀察到都是跟cycle相關的情境，這個時候看著題目還是很難想到要怎麼使用快慢指針去處理，別急! 先把快慢指針放一邊，我們來看看Floyd判圈算法(Floyd Cycle Detection Algorithm)。
Floyd判圈算法最大的重點就是，如果在一個linked list上可以找到cycle，那麼你讓快慢指針一起從linked list的首個節點出發，快慢指針分別以不同的速度前進，兩指針必定會在某個時間點相遇。

咦?這個應該不用特別提醒吧?問題是相遇點在哪?要如何利用相遇點去找到cycle的起始點?
請見下圖，node 1為cycle起始點，node 2為兩指針相遇點，假設快指針的移動速度為慢指針的2倍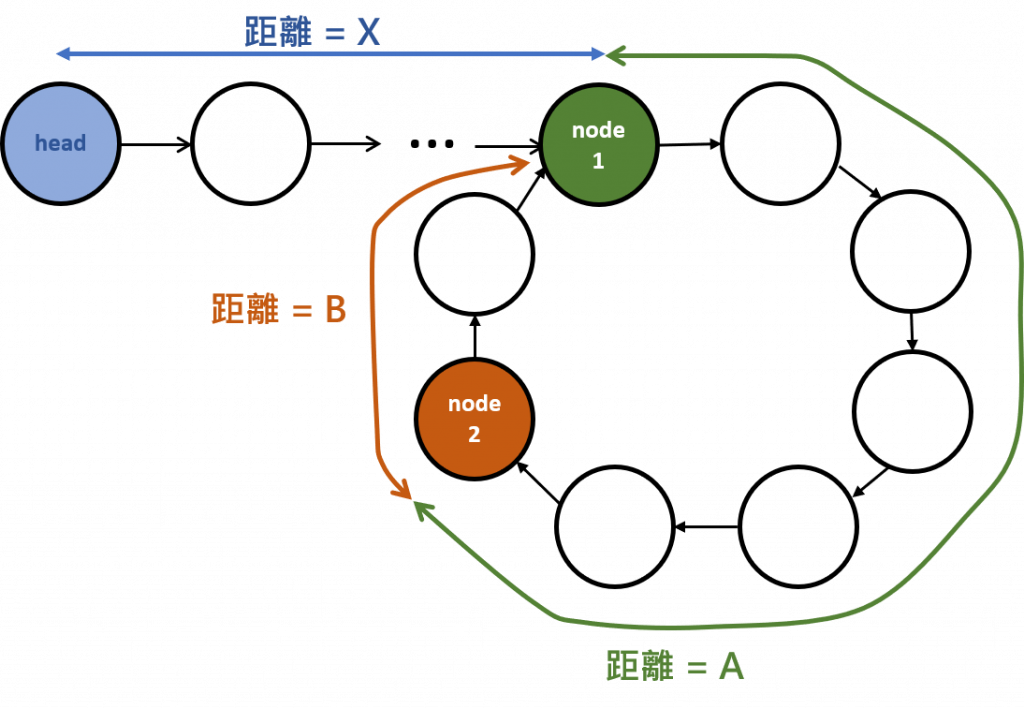

1.如上圖示:
慢指針走的步數 * 2 = 快指針走的步數
2 * (X+A) = X+2A+B
得到→ X = B

2.承上，因X=B代表
只要慢指針從head出發走X步、快指針從node 2(相遇點)出發走B步，
也就是兩指針走相同距離便會在node 1相遇(cycle起始點)
先得到相遇點node 2，再從node 2 去找到node 1 ，便找到cycle的起始點，找到cycle的起始點，就可以進一步取得cycle的長度了。

以上是今天的學習紀錄，晚安各位。 Have a nice dream.

Reference:
BTW,這篇文章讓我豁然開朗，也許你也想看看 → https://hackmd.io/@PeterLei/leetcode142
https://medium.com/%E6%8A%80%E8%A1%93%E7%AD%86%E8%A8%98/%E6%BC%94%E7%AE%97%E6%B3%95%E7%AD%86%E8%A8%98%E7%B3%BB%E5%88%97-two-pointer-%E8%88%87sliding-window-8742f45f3f55

https://www.google.com/search?q=Floyd+Cycle+Detection+Algorithm&rlz=1C1SQJL_enTW879TW881&oq=Floyd+Cycle+Detection+Algorithm&gs_lcrp=EgZjaHJvbWUqDggAEEUYJxg7GIAEGIoFMg4IABBFGCcYOxiABBiKBTIGCAEQRRhAMgcIAhAAGIAEMgcIAxAAGIAEMgcIBBAAGIAEMgcIBRAAGIAEMgYIBhBFGDwyBggHEEUYPNIBBzk3MWowajeoAgCwAgA&sourceid=chrome&ie=UTF-8

https://juejin.cn/post/7206511128277270583

https://zh.wikipedia.org/zh-tw/Floyd%E5%88%A4%E5%9C%88%E7%AE%97%E6%B3%95>