逆元

上一篇文章有大概提了逆元(反元素)的概念，這邊再簡單複習一下

1. 加法逆元：加法逆元的單位元是0，也就是說，對於任何整數 a，a + (-a) ≡ 0 (mod n)。
2. 乘法逆元：乘法逆元的單位元是1，即對於任何整數 a，如果存在整數 x 使得 a * x ≡ 1 (mod n)，那麼 x 就是 a 的乘法逆元。

乘法逆元

如果 a 與 n 互質（即 a 和 n 的最大公因數為1），那麼存在整數 x 和 y 使得：** ax + ny = 1 。
在模運算 mod n 的情況下，因為 ny 是 n 的倍數，所以可以簡化為： ** ax ≡ 1 (mod n)

所以，x 就是 a 在模 n 下的乘法逆元。換句話說，只要 a 與 n 互質，a 必定存在乘法逆元 x。

以下以 mod 7 為例子:
a^(-1)表示a的逆元(與a相乘=1)

• 1^(-1) = 1，因為 1 * 1 ≡ 1 (mod 7)
• 2^(-1) = 4，因為 2 * 4 ≡ 1 (mod 7)
• 3^(-1) = 5，因為 3 * 5 ≡ 1 (mod 7)

回到題目

Modular Inverting

https://cryptohack.org/courses/modular/mdiv/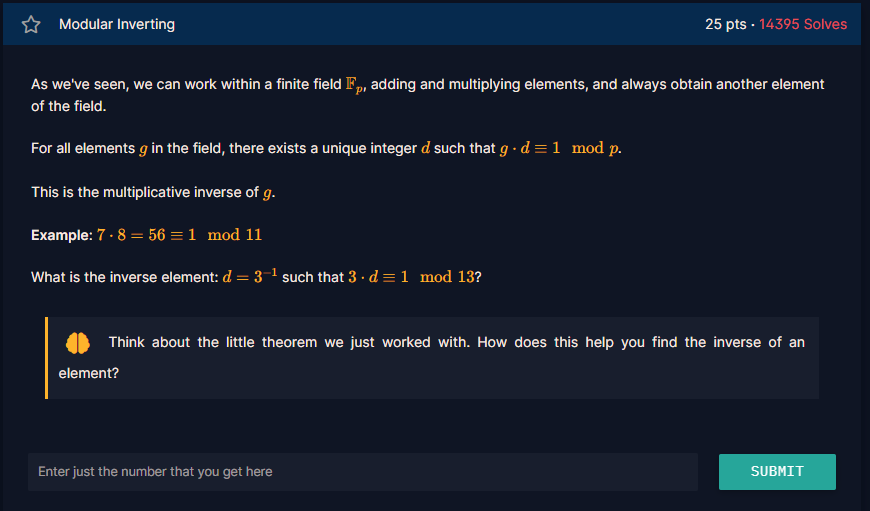

題意:

探討模運算中的乘法逆元的概念，並要我們求3在模13下的乘法逆元d，也就是找到一個d，使得 3 * d ≡ 1 (mod 13)。

解題過程:

方法一:(我想的)
依序尋找 %13==1的數(1不斷+13)，可其中可以整除3的數就是答案啦~
逐次逼近法、線性搜索法，尋找最小的 i，使得 i ≡ 1 (mod 3)。
較為直觀的簡單方法，但當模數很大，這種方法的效率會很低。

### 求3的模反數
# 3　*　d　≡　1　mod　13

i=1
while(i%3!=0):
    i+=13
else:
    print(i//3)

9

方法二:費馬小定理

費馬小定理陳述：如果 p 是質數，且a與p互質，那麼 a^(p-1) ≡ 1 (mod p)。
而在這題中，p = 13（質數），a = 3，且 gcd(a,p)=1。

根據費馬小定理，可得：3^12 ≡ 1 (mod 13)
將兩邊同乘 3^-1（3 的模 13 逆元)，得：** 3^11 ≡ 3^-1 (mod 13) **
接下來只需要計算 3^11 mod 13 就可以求出d了。

print(3**11%13)

9

方法三:
使用函式庫中的工具

###求3的模反數
from Crypto.Util.number import inverse
print(inverse(3,13))

9

參考資料

wiki: https://zh.wikipedia.org/zh-tw/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0
前人的文章: https://ithelp.ithome.com.tw/articles/10323070
模反元素文章: https://medium.com/algorithm-solving/modular-multiplicative-inverse-333ab622d886

後話

今天先寫到這，最近的內容涉及到數論以及一些數學知識，理解以及整理起來都比較費時，如果之後比較有空的話可能會多寫一點。