Given an array of points where points[i] = [xᵢ, yᵢ] represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).
The distance between two points on the X-Y plane is the Euclidean distance (i.e., √(x1 - x2)² + (y1 - y2)²).
You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

給定一個點陣列，其中 points[i] = [xᵢ, yᵢ] 表示 X-Y 平面上的一個點，以及一個整數 k，回傳離原點 (0, 0) 最近的 k 個點。

在 X-Y 平面上兩點之間的距離是歐幾里得距離（即 √((x1 - x2)² + (y1 - y2)²)）。

你可以以任意排序回傳答案。答案保證是唯一的（除了排序以外）。

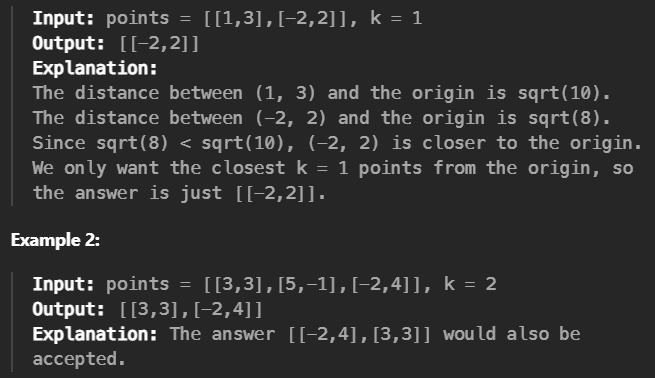
簡單的說，就是把陣列中的每一組的(x,y)算出距離原點的距離，找出k個最小的組合。這次改用max-heap，一樣先建立一個可以裝入k個元素的max-heap，然後再用for loop把剩餘的(x,y)組合(就是整個陣列扣除k組組合)比較距離原點的大小，只要距離比heap的根節點存放的組合還要小，則交換。

注意: 是比根節點小才跟根節點交換，必須讓heap的size保持在k，因為在這個max-heap裡面裝的就是我們要找的k隔離原點最近的組合們。

如此一來，這樣比到最後，直接把heap裡面的組合回傳就完成啦!

是不是很有趣呢? 昨天的題目要找第k個大的元素，使用的是min-heap(最小堆積)，但是今天要找k個最小的組合，使用的卻是max-heap(最大堆積)。

來看程式碼吧

function kClosest(points, k) {
    const maxHeap = [];

    // 交换
    function swap(i, j) {
        [maxHeap[i], maxHeap[j]] = [maxHeap[j], maxHeap[i]];
    }

    // heapify 向上交換
    function heapifyUp(index) {
        const parentIndex = Math.floor((index - 1) / 2);
        if (parentIndex >= 0 && maxHeap[parentIndex][2] < maxHeap[index][2]) {
            swap(parentIndex, index);
            heapifyUp(parentIndex);
        }
    }

    // heapify 向上交換
    function heapifyDown(index) {
        const leftChildIndex = 2 * index + 1;
        const rightChildIndex = 2 * index + 2;
        let largest = index;

        if (leftChildIndex < maxHeap.length && maxHeap[leftChildIndex][2] > maxHeap[largest][2]) {
            largest = leftChildIndex;
        }

        if (rightChildIndex < maxHeap.length && maxHeap[rightChildIndex][2] > maxHeap[largest][2]) {
            largest = rightChildIndex;
        }

        if (largest !== index) {
            swap(index, largest);
            heapifyDown(largest);
        }
    }

    // 插入到heap中
    function insert(point) {
        maxHeap.push(point);
        heapifyUp(maxHeap.length - 1);
    }

    // 删除heap的根節點并保持heap的結構
    function removeTop() {
        if (maxHeap.length > 1) {
            swap(0, maxHeap.length - 1);
        }
        const removed = maxHeap.pop();
        heapifyDown(0);
        return removed;
    }

    // 遍歷所有點並build heap
    for (let [x, y] of points) {
        const dist = x * x + y * y; // 計算距離的平方
        insert([x, y, dist]);

        // 如果heap的大小超過 k，移除root根節點
        if (maxHeap.length > k) {
            removeTop();
        }
    }
    return maxHeap.map(item => [item[0], item[1]]);
}