[30天LeetCode挑戰] 01前情提要與刷題策略+BigO複雜度與DFS/BFS筆記

2024 iThome 鐵人賽

DAY 1

佛心分享-刷題不只是刷題

[30天LeetCode挑戰] 每天一點演算法，讓技巧融會貫通系列第 1 篇

16th鐵人賽

很懶欸

2024-09-15 13:04:57

71 瀏覽

分享至

前情提要

今天是挑戰的第一天，先來歸納一下我這30天內需要達成的目標及挑戰內容，並從我的背景開始講起。

本身畢業於電子工程系，經常使用Python等語言進行開發，但是並沒有系統地學習過演算法。截止目前，我大概刷過30道Leetcode題目，主要集中在Easy難度的題目，Medium難度的題目只占不到5%。這次參加挑戰的目標是希望能夠系統化地學習演算法，並在30天內大幅提升自己的解題能力。

刷題策略制定

這次挑戰我決定將題目按照所涉及的演算法類型進行分類，並在每天刷完題目後撰寫演算法筆記，來加深對演算法的理解與記憶。

學習順序將參考以下的演算法主題圖表：演算法主題學習順序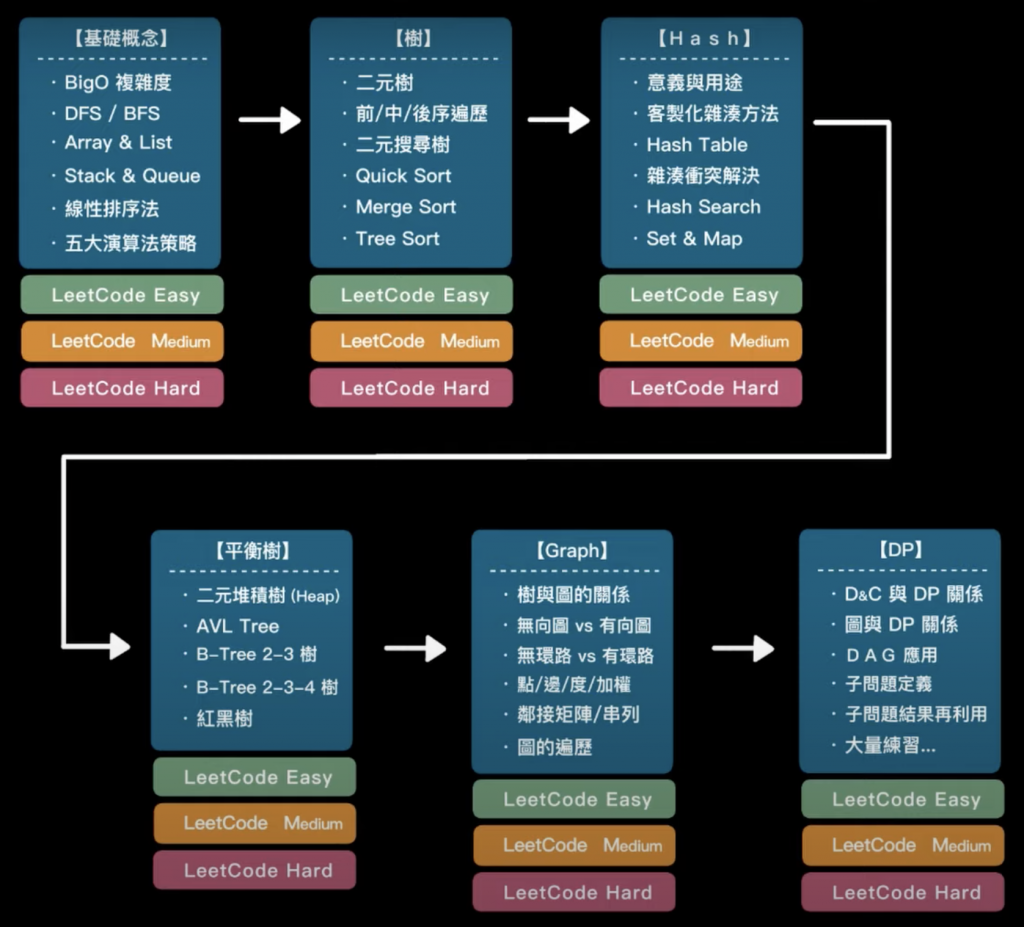

圖片來源：https://www.youtube.com/watch?v=BkKRSMeqoYA

在這30天裡，我希望能夠完全掌握圖片中前四個主題：基礎概念、樹、Hash、平衡樹。我將以每週學習一個主題為目標，而主題的開始都定在假日，這樣可以利用更多的時間來學習概念、理解演算法。

計劃與規則：
由於每天的進度可能會有所不同，我不想提前規劃出固定的每日進度表，而是根據每天的進展動態調整進度，因此我為自己制定了以下幾個挑戰規則：

每週學習完成一個主題，一個月共涵蓋四個主題。
每天至少刷一道Leetcode題目，並從開始執行。
每刷3題Easy，需要刷1題Medium。
在學習與查找資料的過程中，需要將重點整理成筆記，並記錄下相關的連結，方便日後複習與查閱。

這樣的安排可以讓我更靈活地學習，也能確保每一天都在進步，並且逐步達成挑戰的目標。
OK馬上進度挑戰的第一天！！！

Big O複雜度

Big O目的：計算簡化版的演算法效能
計算標的：以步驟為計算標的，不以時間
特色：簡化所有常數、省略低次方

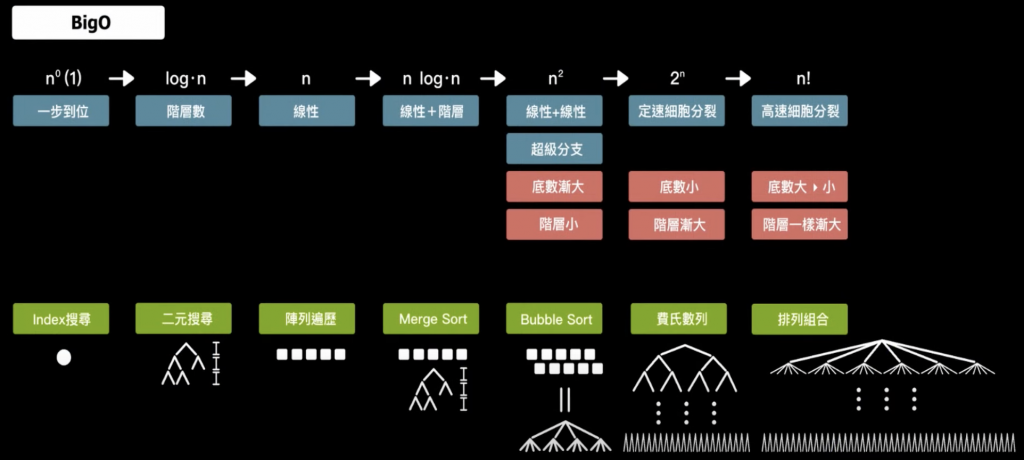
學習影片：https://www.youtube.com/watch?v=es82PRNCn9I

如上圖列出演算法品質由低至高，總結如下：

O(1)：常數時間複雜度。不論輸入資料量多少，演算法的執行步驟始終固定。
O(log n)：對數時間複雜度。常見於二分搜尋，當資料量增加時，步驟的增長速度非常緩慢。
O(n)：線性時間複雜度。步驟數與資料量成正比，資料量翻倍，步驟也翻倍。
O(n log n)：常見於排序演算法，如合併排序與快速排序。
O(n²)：平方時間複雜度。常見於雙重迴圈的演算法，如暴力解法。
O(2ⁿ)：指數時間複雜度。此類演算法隨著資料量的增加，執行步驟會急劇增長。
O(n!)：階乘時間複雜度。常見於排列組合問題，這類演算法隨著資料量增加，效能會極度低下。

在實際開發中，選擇合適的演算法是非常重要的。即便是同一問題，不同的演算法其 Big O 表現可能差異巨大，這也是學習演算法的重點：學習並理解各種演算法的時間複雜度，並在解題時作出最優的選擇，當然這只是先理解基本概念，詳細的應用在之後的刷題應該都會用到。

DFS/BFS

BFS 和 DFS 是圖或樹結構中兩種常見的遍歷方式，常用來搜索資料或解決問題。

學習影片：https://www.youtube.com/watch?v=oLtvUWpAnTQ

BFS (Breadth First Search) - 寬度優先搜索

BFS 會先遍歷每一層的節點，再逐層向外擴展。它會先訪問最接近起點的節點，然後再訪問更遠的節點。

BFS 實現方式：
使用隊列（Queue）來儲存下一步要訪問的節點。
步驟：
把起始節點加入隊列。
從隊列取出節點，訪問它的鄰居，並將未訪問過的鄰居加入隊列。
重複此過程，直到隊列為空。

def bfs(graph, start):
    visited = set()  # 用來記錄已訪問的節點
    queue = [start]  # 使用 list 來當作隊列
    visited.add(start)

    while queue:
        node = queue.pop(0)  # 從隊列中取出第一個元素（起始節點）
        print(node)  # 進行訪問

        # 訪問該節點的所有鄰居
        for neighbor in graph[node]:
            if neighbor not in visited:
                visited.add(neighbor)  # 標記鄰居已訪問
                queue.append(neighbor)  # 將未訪問的鄰居加入隊列

DFS (Depth First Search) - 深度優先搜索

DFS 會先沿著一條路徑一直走到底，再回頭尋找其他路徑。它會優先深入每條路徑，直到走不通再回溯。

DFS 實現方式：
使用堆疊（Stack）或遞迴來實現。
步驟：
從起點開始，訪問節點並標記為已訪問。
依序訪問鄰居節點，直到所有鄰居都被訪問。
若走到盡頭，回到上一層繼續尋找未訪問的鄰居。
Stack方法：

def dfs(graph, start):
    visited = set()  # 記錄已訪問的節點
    stack = [start]  # 使用 list 作為堆疊，初始放入起點

    while stack:
        node = stack.pop()  # 從堆疊中取出當前節點
        if node not in visited:
            print(node)  # 訪問該節點
            visited.add(node)  # 標記節點為已訪問
            
            # 將鄰居節點加入堆疊（未訪問過的節點）
            for neighbor in graph[node]:
                if neighbor not in visited:
                    stack.append(neighbor)

使用遞迴的方法：

def dfs_stack(graph, start):
    visited = set()
    stack = [start]  # 使用一個堆疊來模擬調用棧
    
    while stack:
        node = stack.pop()  # 從堆疊中取出當前節點
        if node not in visited:
            visited.add(node)  # 訪問當前節點
            print(node)
            
            # 將鄰居節點推入堆疊
            for neighbor in graph[node]:
                if neighbor not in visited:
                    stack.append(neighbor)

因爲 DFS 深入並回溯的特性，因此適合遞迴操作，而 BFS 需要隊列逐層遍歷，不適合用遞迴。

好像有做過類似的題目，但那時候對於這個觀念沒有那麼熟悉，這次經過學習後徹底理解了 BFS 和 DFS 的原理與差異，尤其是如何有效運用 Stack（堆疊）和 Queue（隊列）來實現這兩種遍歷方法，至於Stack（堆疊）和 Queue（隊列）在之後的筆記會提到，再詳細講解。

104. Maximum Depth of Binary Tree

Stack方法：

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:  # 如果樹是空的，深度為0
            return 0
        
        stack = [(root, 1)]  # 堆疊保存 (節點, 深度) 元組
        max_depth = 0

        while stack:
            node, depth = stack.pop()  # 取出當前節點和深度
            
            if node:
                max_depth = max(max_depth, depth)  # 更新最大深度
                # 注意：先將右子節點壓入堆疊，再壓入左子節點
                # 這樣左子節點會先被處理，符合 DFS 的特性
                stack.append((node.right, depth + 1))
                stack.append((node.left, depth + 1))
        
        return max_depth

遞迴方法：

def maxDepth(self, root):
    """
    :type root: TreeNode
    :rtype: int
    """
    if not root:  # 如果樹是空的，深度為0
        return 0

    # 遞迴計算左子樹和右子樹的最大深度
    left_depth = self.maxDepth(root.left)
    right_depth = self.maxDepth(root.right)

    # 返回較大的深度並加上當前節點的深度（1）
    return max(left_depth, right_depth) + 1