動態規劃（Dynamic Programming） 動態規劃是一種有效率計算由子問題堆疊而成的演算法，是一種常見的解題方式。透過將問題分解成許多可以利用簡單方法解決的子問題，將其逐一解出並記錄，透過此方式來解答複雜的問題。其精神在於 「同樣的問題不要再算第二次」 ，而這樣的演算法也是在解決許多重疊子問題的複雜問題最有效。當遇到複雜計算的問題不知如何下手時，試著將問題動態規劃分解成一個個能夠解決的子問題，找到問題之間的規律，並且將解決後的答案記錄下來，在後續遇到需使用前一次計算出來的答案時就可以直接查表並給出答案。利用空間換取時間的解題方式，就是動態規劃。

範例說明

動態規劃中最經典的問題無非是爬階梯問題，總共有n階梯，一次最多能走一階或兩階，問你有多少種方式可以走到第n階？

問題：假設n=5，先將其拆解成：n=1.2.3.4.5四個子問題

• n=1

  解法：[ 1 ] ⇒ 1種

• n=2

  解法：[ 1, 1 ]、[ 2 ] ⇒ 2種

• n=3

  解法：[ 1, 1, 1]、[ 1, 2 ]、[ 2, 1 ] ⇒ 3種

• n=4

  解法：[ 1, 1, 1, 1 ]、[ 2, 1, 1 ]、[ 1, 2, 1 ]、[ 1, 1, 2 ]、[ 2, 2 ] ⇒5種

由上述四種拆解問題可得出：F(3)=F(2)+F(1)=2+1=3種、F(4)=F(3)+F(2)=3+2=5種，可以明顯看出，當今天要計算走到n階有多少種方式這個問題其實就是數學中的費氏數列問題：F(n)=F(n-1)+F(n-2)，故當今天要計算n=5時只需將F(4)+F(3)=8，就可得知最多有8種方式可以走到第5階。

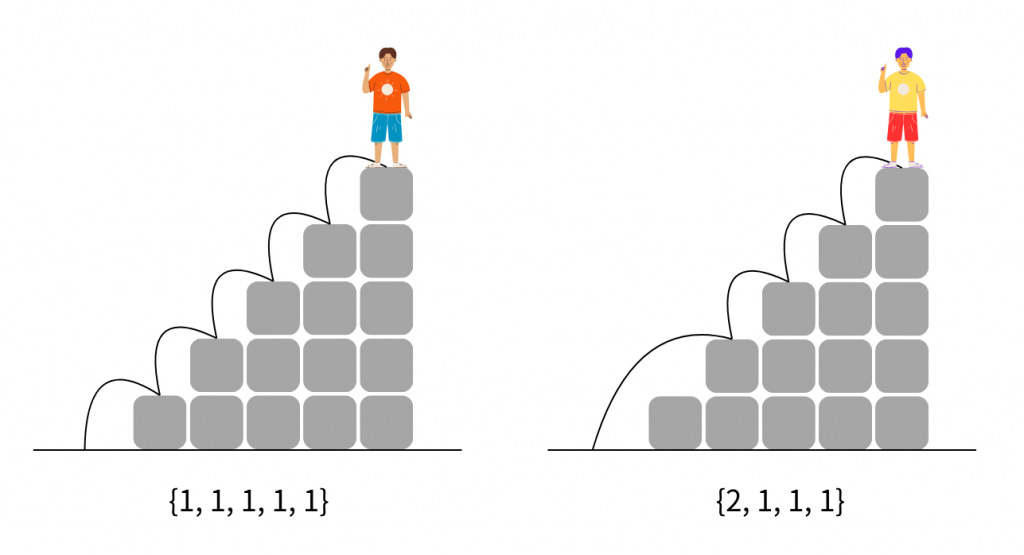
• n=5

  解法：[ 1, 1, 1, 1, 1 ]、[ 2, 1, 1, 1 ]、[ 1, 2, 1, 1 ]、[ 1, 1, 2, 1 ]、[ 1, 1, 1, 2 ]、[ 2, 2, 1 ]、[ 2, 1, 2 ]、[ 1, 2, 2 ] ⇒ 8種

  

優點：

• 解決複雜問題的能力：動態規劃可以有效地解決許多複雜的最佳解問題，特別是那些具有重疊子問題和最佳子結構特性的問題。
• 避免重複計算：通過儲存已計算子問題的結果，動態規劃避免了多次計算相同的子問題，從而顯著提高了效率。
• 系統性的方法：動態規劃提供了一種系統性的方法來解決問題，使得問題的解決過程更為結構化，易於理解和實現。
• 適用於多種問題：適用於許多不同類型的問題，如最短路徑問題、背包問題、序列比對等。

缺點：

• 記憶體消耗：動態規劃通常需要額外的空間來儲存中間計算結果。對於大型問題，這可能會消耗大量的記憶體。
• 複雜度：對於一些問題，動態規劃的實現可能非常複雜，需要仔細設計狀態和解決公式。這可能使得問題的解決過程變得不易理解。
• 時間複雜度：雖然動態規劃通常比簡單的暴力法要高效，但對於某些問題，仍可能需要高時間複雜度，特別是當狀態空間非常大時。
• 問題建立：需要正確地識別問題的最佳子結構和重疊子問題。這對於某些問題來說可能不容易確定，並且需要仔細建立。

參考資料：

1. 演算法筆記系列 — Dynamic programming 動態規劃 - Medium by Sean Chou
2. Ch15 動態規劃 - HackMD by Chu-Ling Ko
3. dynamic programming 演算法筆記 - 國立臺灣師範大學