「我並不認為自己強大,而是還相當的不成熟。大概是可以快速轉換心情吧,但技術上沒有特別優於他人。就算下出了惡手,下了就下下去了、沒有辦法。總之就是思考當時的局面下的最佳手段。......在這世界上,輸棋、事情的發展不如己意是很常見的,在那些情況下,可以多大程度地像是平常一樣去對處,我認為是很重要的。」
-- <井山裕太:七冠王之道>,井山裕太於十段戰勝利取得圍棋史上首次七冠頭銜之後,記者會上的回答。井山裕太.日本棋院出版部著,拙譯。
連續講了幾天 AI、機器學習相關的內容,雖然只有大概四、五篇,但其實可掌控的部份也描述的差不多了。這個部份大部份是實驗、解讀數據、決定下一步怎麼走的努力比較耗費心神,但也因為沒有什麼營養,要寫成文章也還是比較困難。今天開始再把一些主題補完。
從殘局來訓練棋力的概念,並非我所獨創。象棋這種攻殺型的棋種,新手玩家是可以從一般殘局學會蠻多技巧、累積棋感;圍棋的話沒有殘局這個用語,但各個局部類型的死活題,或是以領地結算的終盤官子題,也都是現代圍棋課程的標準配備了。疫途的話,隨著散落棋盤上的標記與區域控制,到了後期戰略目標會越顯固定,展現出有如真劍對決般緊湊的攻殺;讓人很嘔的就是,目前訓練出來的代理人或是隨機猴子,對於這些棋盤上的張力毫無感動,漠然地行棋。
在 DeltaPathogen 專案之中,先前介紹過,代理人使用的 --delay-unit 參數,原本就有意針對較長對局的後續對局手順收集對局資料,也算是一種針對殘局的意識,但是缺乏理論根據。因為就算總體手數很長,可能也只代表棋盤前半局放任隨機猴子亂下、快轉棋局進度的時候,有好些關鍵的局面的走向被無意識地推進;就算結束了 delay,也可能棋局大勢已定,不管模擬次數如何,也未必能收集到什麼有用的資訊之感。所以後期我其實比較少利用這個參數了,但也懶得移除。
在八月底時,也曾經直接面對當時 gen6/gen7 世代的模型,觀察它們推論的弱點。當時是手動過濾一些棋譜,並且手動刪除最後的手數,形成第一次經手的殘局譜。但這個全然手動,非常耗時耗腦。為了加速,設計了棋譜瀏覽器(record_viewer,將於接下來的系列文介紹),並且也才有了在第二天展示的截圖。
後來,在賽期當中,實在是失利太久,終於是決定下手,自動地根據目前已經累積的這些棋譜,自動生成殘局。
切入點是從最後一手開始做起。無論是高端玩家的高棋或是低手互毆的無聊之局,只要逆轉終盤局面、回覆盤面一手,輪到勝方的標準回合的時候,都可以有以下判斷:
這麼做的缺點,除了上述 policy 並非絕對精準之外,還有 value 的單一性。須知,參考書中的 value 標記方法是非常殘酷的:敗方的所有著手經歷過的所有盤面,都會被標記為 -1.0,而勝方的所有著手經歷過的所有盤面,都會被標記為 1.0。我在當時詳讀收集資料章節之後,在開發筆記當中紀錄了大怒、拒絕配合的心情,但隔天又紀錄可以理解但深感懷疑。
可以理解的因素在於一個思想實驗:假若有圍棋之神的存在,那麼祂們的對局過程會類似這樣:
A:「我們來猜先吧。」
B:「好的。」
(兩位猜先之後,A 得黑方先行。)
A:「嗯...」
B:「嗯。是你贏了。」
關於貼目和圍棋之神,可以參考這篇部落格的分析。
這當然是因為兩位神衹都對於所有的變化了然於胸,而且祂們也知道先手握有優勢(在貼目不高的規則下),所以誰得先手,就註定會贏。回頭想像一個已經完全理解疫途的疫途之神,祂當然也是看到任何盤面就能夠立刻知道到底是必勝還是必敗。而在一個神經網路模型已經內建了這些知識的情況下,它當然也要能夠做出這樣的預測;隨著權重慢慢收斂,雙方玩家在自己的盤面也應該會越來越接近一方總是很接近 1.0 且另一方總是很接近 -1.0 的狀況。
順帶一題。有人說 AlphaGo 或絕藝或 Katago 已經是圍棋之神,我會說這很顯然並非如此。現在一般黑貼七目半規則中,起手黑棋勝率約 40~45%,Well,如果它已經把變化都算完,那就應該給一個 0% 出來,因為看到所有著手都知道怎麼應對。
岔題甚遠。總之,value 值的單一會有一個後果,如圖:
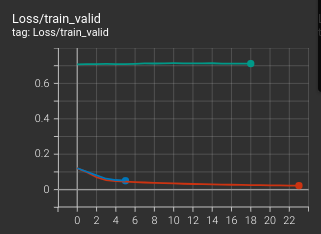
這裡的淺灰色曲線(資料集採用殘局譜與一般對局譜混合的模式)和其他的訓練嘗試不同,幾乎無法隨著訓練而降低損失。所以還是需要有些 value 為 -1.0 的資料才行。
所以我在 patch 當中為倒數第二手新增以下判斷,
// policy
let mut policy = valid.clone();
if num_non_zero > 1 {
if is_map {
policy[[coord.map_to_valid_encode()]] = 0.0;
} else {
policy[[coord.env_to_valid_encode()]] = 0.0;
}
}
// value
// -0.5 is a speculation, that "you are losing!!!"
// but if this is the only option, well, die...
let value = Array::from_shape_fn(
1 as usize,
|_| if num_non_zero > 1 { -0.5 } else { -1.0 } as f32,
);
抱歉,num_non_zero 名子也取得不好,但總之意思是「原本的倒數第二手是不是唯一的選點」的意思。對策略的分佈來說,我也沒有太有野心的計算,就是將原本的選點歸零,畢竟選擇該點將使得下一手面對稍有實力的對手的時候走向敗局。如果該手不是唯一的選點,那這樣的策略製作,就會提昇其他策略的機率。
至於價值判斷,可以確定當該著手即是唯一選擇的時候(else),那當然就應該標記為必敗之局的 -1.0。但如果有其他選點呢?也許其實倒數第二手,原本的敗方有提前取勝之機蘊含在其他選點之中也不一定?這敗值應該如何估計呢?我在這個第一版是估計為 -0.5。想說,既然原本的世界線,敗方認敗,那很有可能它本來就跟失敗比較接近?
但總之這還是太過臆測,所以後來的版本,就直接不猜了,只處理只剩下唯一的著手導致必敗的盤面就好。
像是我的讀取檔案設計得非常怪也不彈性,就是並非在作為字串傳入的資料夾底下撈取棋譜檔來解析,而是在該資料夾下的資料夾之下的棋譜檔。之所有有這樣的結構是因為,在一般的模擬對局收集過程中,我以容器展開在不同資料夾下紀錄資料集與棋譜。
Some(ref dirname) => {
for entry in read_dir(dirname)? { // 這是最上層
let sub_dirname = entry?.path();
// Skip non-directory files
if !sub_dirname.is_dir() { // 這應該是子資料夾?不是的話就跳掉檢查下一個
continue;
}
for filename in read_dir(sub_dirname.clone())? { 然後才在子資料夾下檢查
if let Ok(entry) = filename {
let entry_fn = entry.file_name();
let ret = entry_fn.to_string_lossy().into_owned();
let full_path = Path::new(&sub_dirname).join(&ret);
let full_path_str = full_path.display().to_string(); // 看這精美的層層轉換才能變成一個可以用的字串... 寫完就忘了
if !re.is_match(&full_path_str) { // `re` 是更早略過的棋譜副檔名的模式
continue;
}
總之,這樣的小工具,搭配大量生成的隨機對局方法,就可以大量生成殘局譜,而且比起一般模擬對局的蒐集快很多。以結果來說,我在第六日開始提及的這個工具。但是,這個方法收集來的資料集很難嵌入 AlphaZero 的精神,因為它與逐漸改良的代理人自我對局,似乎扯不上關係。或者另外一個角度,如果是從自我對局當中收集殘局,效率非常的低,因為一局遊戲平均回合數約 30(至少以現階段實力都還很接近隨機猴子的階段),裡面殘局譜能鎖定的也只有最多兩個回合而已。
以上的本日內文,展示了為什麼過去幾天的目前狀況所更新的訓練進度中, gen16 反覆被強調提及。並且,導入這個機制之後訓練出來的代理人的驗證遊玩的效果令人振奮的。而且看起來,可以以這個為基礎持續用普通對局的資料來迭代。
但是不到一週,我又開始懷疑這個手段。訓練過程中發現,gen19-trial2 似乎更有可能是從頭開始訓練的,而非我原先以為從 gen16 的殘局譜衍生而來的。因為我在這一輪(gen20)的訓練當中,只要是從先前繼承的模型(紅色與洋紅色),就跑不出那種曲線。反倒是從頭開始的 trial4(淺灰色)有與 gen19-trial2 (藍色)相仿的訓練歷程。如圖
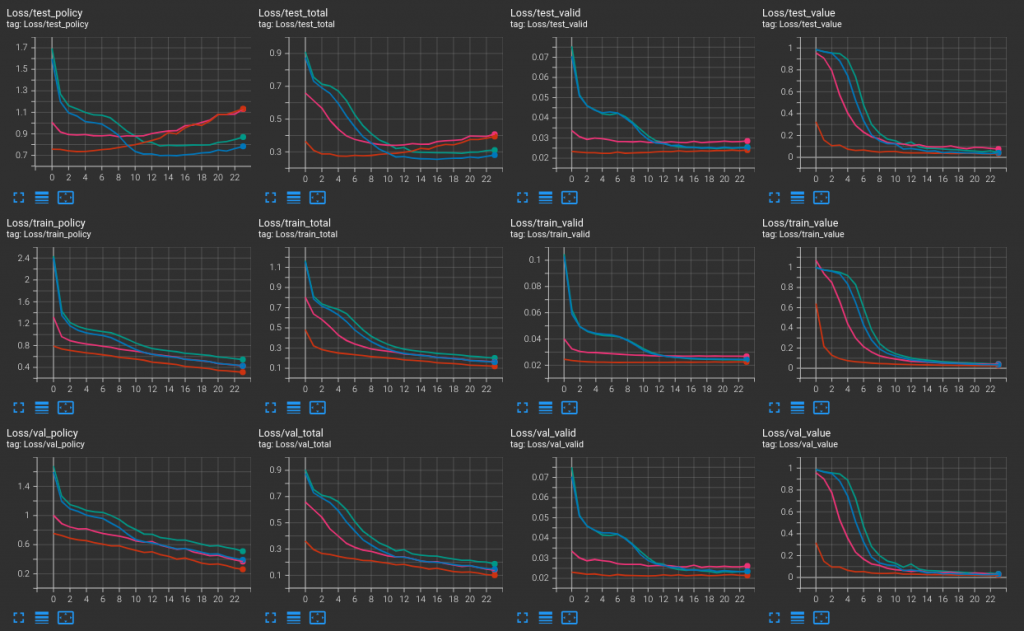
那接下來,下一輪的模擬,又應該收集怎麼樣的對局比較好呢?這需要沉思一下。今天引述曾是日本圍棋第一人的井山裕太於奪得七大頭銜時的訪問,連那樣強大的人都認為平常以對最為重要,那接下來也不該怨歎什麼,總之是各種手段都試試吧。
另一方面,這次在 gen20 當中,累積了三組不同的驗證遊玩。其中可以看到,無論是哪個訓練出來的模型,作為疫病方對 random,效果都可以比 random 的疫病還要好了。而且,看起來,以 random 對 random 當作 baseline 的作法可能也快要成為過去式了,因為我們展示了不管是怎樣的對戰組合,都不太可能呈現 random 對 random 的那種勝率。看起來,稍有知識的代理人互相對決的話,疫病方是較佔優的。
