前言

嘿嘿～剛好今天下雨，想不想知道大雨過後水都積在哪裡呢？
這次我們要來解一道超經典的題目——Trapping Rain Water（接雨水問題）！

這題可是 Leetcode 上有名的 Hard 題，但別被嚇到，因為我們會帶你一步一步解鎖，輕鬆搞懂這個有趣的挑戰！

想像一下，下雨過後，地面高高低低的地方會積滿水，就像解一場雨水積水的小謎題～
這題的精髓在於找出地形凹陷能存多少水，是不是感覺很酷？
跟我一起來，一起探索這場神奇的「接雨水」之旅吧！

題目 Trapping Rain Water

難度：Hard

題目描述：

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

給定 n 個非負整數表示高程圖，每個柱子的寬度為 1，請計算這些柱子之間能夠接住多少雨水。

範例 1：

輸入： height = [0,1,0,2,1,0,1,3,2,1,2,1]

輸出： 6

說明： 圖中黑色部分代表高程圖，由陣列 [0,1,0,2,1,0,1,3,2,1,2,1] 表示。可以看到藍色部分是被困住的雨水，一共 6 單位的水量。

範例 2：

輸入： height = [4,2,0,3,2,5]

輸出： 9

實作

這題目聽起來有點複雜，但其實重點是找到每個位置左邊和右邊的最大高度，然後算出該位置能接的水量！我們來看看以下的程式碼解法：

function trap(height: number[]): number {
    let left = 0, right = height.length - 1;
    let leftMax = 0, rightMax = 0;
    let waterTrapped = 0;

    while (left < right) {
        if (height[left] < height[right]) {
            height[left] >= leftMax ? (leftMax = height[left]) : (waterTrapped += leftMax - height[left]);
            left++;
        } else {
            height[right] >= rightMax ? (rightMax = height[right]) : (waterTrapped += rightMax - height[right]);
            right--;
        }
    }
    return waterTrapped;
}

解釋

1. 雙指針法：這個方法非常聰明，我們設置兩個指針 left 和 right，分別從陣列的兩端開始往中間走。
2. 追蹤最大高度：我們維護 leftMax 和 rightMax 兩個變數，分別追蹤當前左邊和右邊的最大高度。
3. 水量計算：當 height[left] < height[right] 時，我們移動左指針，更新左側最大高度，並計算當前點能積的水。同理，當右指針小時就更新右側。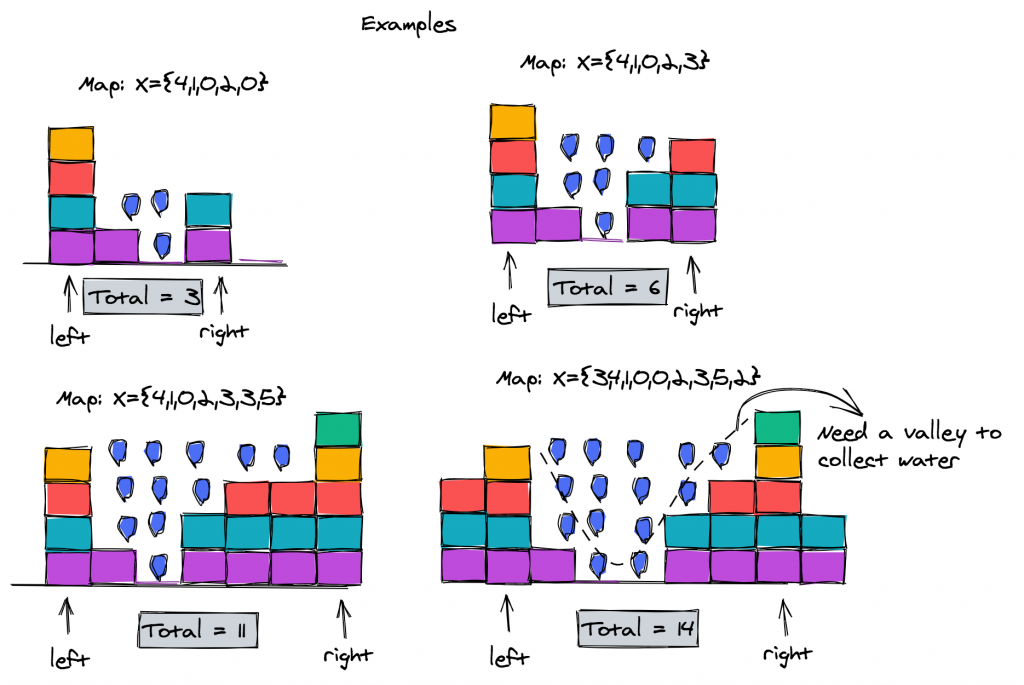
4. 不重複計算：這種方法確保我們每次只會根據較小的一邊來進行水量計算，避免重複或錯誤的判斷。

思路心法

1. 使用雙指針法，從兩邊開始進行水量計算

   這題的核心是找出每個位置上能積多少雨水，但逐個位置去計算左邊和右邊的最大高度可能會導致時間複雜度太高。我們用雙指針法來優化這個過程：

   • 設置兩個指針：一個 left 指針從陣列最左邊開始，一個 right 指針從最右邊開始。
   • 這樣做的好處是，我們可以同時從左右兩邊向中間移動，每次只處理較低的那一邊，避免重複計算並快速找到能儲水的空間。

2. 動態更新左右兩邊的最大高度，確保計算的正確性

   當我們在移動指針時，需要記錄目前 left 和 right 指針經過的最大高度，分別用 leftMax 和 rightMax 來追蹤：

   • leftMax 記錄 left 指針從最左端到目前位置的最高高度。
   • rightMax 記錄 right 指針從最右端到目前位置的最高高度。

   每次移動指針時，我們都會比較目前的高度和 leftMax 或 rightMax：

   • 如果當前高度比最大高度低，表示這裡會形成凹陷，可以積水。
   • 我們就可以計算當前的積水量為 maxHeight - height[current]，這樣確保水不會從高處流出去。

3. 善用條件判斷來計算雨水，左右指針交會時結束

   • 當 left 指針所指的高度低於 right 指針時，我們會移動 left 指針，因為左邊的高度限制了積水的上限。
   • 反之，如果 right 指針所指的高度較低，則移動 right 指針，這樣每次都能找到可以積水的低點。
   • 當兩個指針相遇時，我們就完成了對整個高度圖的計算，因為此時所有的可能積水區域都已經被處理過了。

為什麼這樣處理？

這樣做的核心原因是最大化效率：我們利用雙指針同時從兩邊縮進來，快速跳過沒有積水的區域，並動態更新最大高度，避免重複計算。這種方法將時間複雜度降低到 O(n)，是非常高效的解法。

透過逐步比較和更新左右邊界的高度，保證我們能正確計算出每一格的積水量，而不用額外的空間或時間來追蹤所有位置的狀態。

本次要點：

• 運用雙指針優化解法，降低複雜度。
• 動態更新左右邊界最大值。
• 維持計算水量的準確性，避免重複累加。

這樣解完這題後，是不是覺得雨水計算沒那麼可怕啦？掌握這些思路之後，碰到類似的問題也能輕鬆應對囉～

希望這篇文章對大家有所幫助，繼續努力！我們下次再見～(≧∇≦)/