堆疊演算法（Stack） 是一種有序串列（即一群相同資料型態的組合），具有「後進先出」（Last In First Out, LIFO）的特性，故其所有的動作、資料的處理方式均在同一邊進行。而日常生活中處處可見堆疊的例子，例如將眾多書本裝箱後，若需要取出其中某一本書，就必須從最上面那本開始取出。像是這樣的例子在生活中常見，而以下將針對堆疊的定義、專有名詞、在算術上的運用等等概念進行說明和舉例介紹。

堆疊的定義整理

1. 一群相同資料型態的組合，即有序串列。
2. 具有「後進先出」（Last In First Out, LIFO）的特性。
3. 將一元素放入堆疊頂端，此動作稱為push（加入）。
4. 將一元素從堆疊頂端拿出，此動作稱為pop（取出）。
5. push和pop這兩種動作皆發生於同一端，此端稱為top（頂端）。
6. 取出資料時僅能從top端取出，無法從中間取出。

堆疊常用名詞

堆疊在算術上的運用

在日常生活中，我們所使用的四則運算都屬於中序（infix order）運算式，意思就是運算子位於兩個運算元之間的表示法（A+B），而算術式可以表示為中序表示法（A+B）、前序表示法（+AB）和後序表示法（AB+）。由於中序表示法可能會含有括號，所以日常生活常用的中序式並不能直接的為電腦所用。因此，若要使用電腦來處理運算式，必須先將中序式轉換為後序式。以下的範例說明將針對「中序式轉換成前序式」兩種表示方法間的轉換與堆疊之關聯作說明：

【補充】常見的運算子優先順序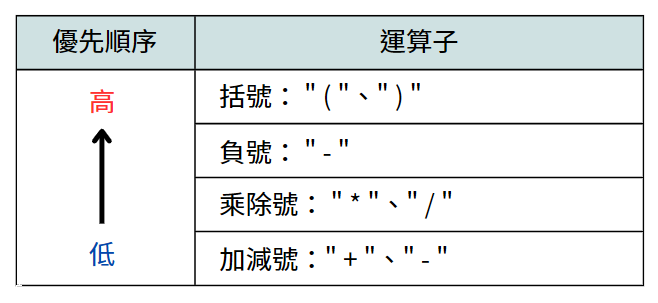

範例說明

• 中序式轉換成前序式

  • Tips:

    • 「由右而左」掃描資料。
    • 遇到運算元，直接輸出。
    • 遇到運算子，則：
      
    • 若運算式讀取完畢仍有運算子存於堆疊中，依序由頂端輸出。
    • 最後須反轉輸出的字串。

  • 運算式：A+B*C-D

  • Step1：讀取 ” ) ” ，放入堆疊。

    此時堆疊：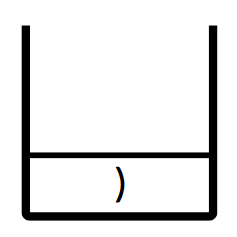
    

  • Step2：讀取 ” D ” ，直接輸出。

    此時輸出字串：D

  • Step3：讀取 ” - ” ，放入堆疊。

    此時堆疊：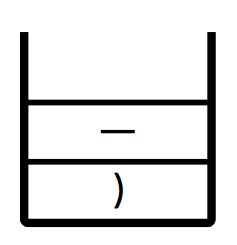
    

  • Step4：讀取 ” C ” ，直接輸出。

    此時輸出字串：DC

  • Step5：讀取 ” ( ” ，依序輸出堆疊中運算子直到取出 ” ) ”。

    此時堆疊：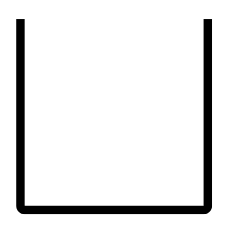
    

    此時輸出字串：DC-

  • Step6：讀取 ” * ” ，放入堆疊。

    此時堆疊：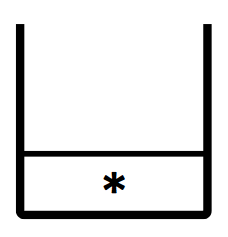
    

  • Step7：讀取 ” B ” ，直接輸出。

    此時輸出字串：DC-B

  • Step8：讀取 ” + ” ，小於 ” * ” 優先權，將 ” * ” 輸出並將” + ” 放入堆疊。

    此時堆疊：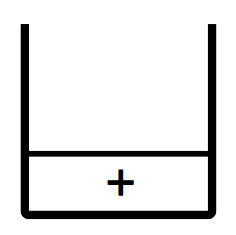
    

    此時輸出字串：DC-B*

  • Step9：讀取 ” A ” ，直接輸出。

    此時輸出字串：DC-B*A

  • Step10：運算式讀取完成，將堆疊中所有運算子依序輸出。

    此時堆疊：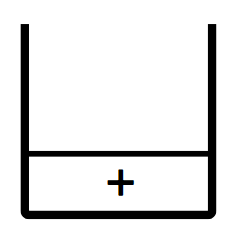
    

    此時輸出字串：DC-B*A+

  • Step11：反轉輸出的字串。

    最終結果字串：+A*B-CD

• 中序式轉換成後序式

  • Tips:
    • 「由左而右」掃描資料。
    • 遇到運算元，直接輸出。
    • 遇到運算子，則：
      
    • 若運算式讀取完畢仍有運算子存於堆疊中，依序由頂端輸出。

優點：

• 簡單易用：堆疊的操作非常簡單，只有兩個主要操作——加入（Push）和取出（Pop），這使得它易於實現和使用。
• 記憶體管理：堆疊可以自然地用於處理函數呼叫和遞迴問題。每次函數呼叫，系統會自動將相關的變數加入堆疊，函數結束時自動取出，方便記憶體管理。
• 反向操作：堆疊非常適合需要反向處理的問題，例如字串反轉、深度優先搜尋（DFS）等問題。
• 運算符處理：在處理表達式計算時（如中序式轉前序式），堆疊是一種非常有效的工具。

缺點：

• 容量限制：如果使用固定大小的陣列來實現堆疊，當數據超過陣列大小時，會導致溢出（Overflow）問題。
• 隨機存取不便：堆疊只能訪問頂端元素，無法隨機存取中間或底部的數據，因此不適合需要頻繁隨機存取的場景。
• 效率問題：在某些情況下，使用堆疊可能會帶來額外的空間和時間開銷，特別是深度遞迴可能導致堆疊溢出（Stack Overflow）問題。

參考資料：

1. 吳燦銘、胡昭民(2018)。《圖解資料結構-使用Java(第三版)》。新北：博碩文化。
2. 吳燦銘、胡昭民(2020)。《圖說演算法：使用Java》。新北：博碩文化。