在本節中,我們將探索如何使用現代深度學習模型——Transformer,進行股票價格的預測。我們將使用昨天中用於 LSTM 的相同數據,即蘋果公司(AAPL)的股票數據,並使用 PyTorch 框架實現 Transformer 模型。我們將從數據預處理、模型構建、訓練到評估,完整地演示如何應用 Transformer 模型進行股票價格預測。今日 Colab
Transformer:最初在自然語言處理領域取得了巨大的成功,擅長處理序列數據,能夠捕捉長距離的依賴關係。
自注意力機制(Self-Attention):Transformer 的核心,允許模型在計算時關注序列中的不同位置,捕捉複雜的時間依賴性。
我們將利用 Transformer 的這些特性,應用於股票價格的時間序列預測。
自注意力機制(Self-Attention):能夠讓模型在計算時關注序列中的不同位置,捕捉長距離依賴。
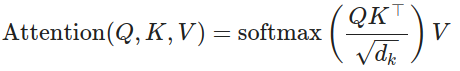
多頭注意力機制(Multi-Head Attention):通過並行計算多個自注意力,捕捉不同的特徵子空間。
Transformer 能夠捕捉價格隨時間的變化模式。Transformer 有能力建模這些關係。使用第15天中相同的數據,即 AAPL 股票的歷史收盤價,如果是接續從昨日看過來的可以跳過這一節。
import pandas as pd
import numpy as np
import yfinance as yf
# 獲取數據
data = yf.download('AAPL', start='2015-01-01', end='2021-01-01')
# 提取收盤價
data = data[['Adj Close']]
data.rename(columns={'Adj Close': 'Close'}, inplace=True)
請參照昨天,這邊就暫不浪費篇幅放圖了。
為了提高模型訓練的效率,我們需要將數據歸一化到 [0, 1] 區間。
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
data['Close'] = scaler.fit_transform(data[['Close']])
將時間序列轉換為模型可接受的輸入格式。
def create_sequences(dataset, lookback=60):
X, y = [], []
for i in range(len(dataset) - lookback):
X.append(dataset[i:(i + lookback), 0])
y.append(dataset[i + lookback, 0])
return np.array(X), np.array(y)
# 轉換為 numpy 陣列
dataset = data.values
# 定義 lookback 窗口大小
lookback = 60
X, y = create_sequences(dataset, lookback)
# 劃分比例
train_size = int(len(X) * 0.8)
test_size = len(X) - train_size
X_train = X[:train_size]
y_train = y[:train_size]
X_test = X[train_size:]
y_test = y[train_size:]
Transformer 模型需要輸入形狀為 (seq_length, batch_size, feature_size)。
# 將數據轉換為 PyTorch 張量
import torch
X_train_tensor = torch.from_numpy(X_train).float()
y_train_tensor = torch.from_numpy(y_train).float()
X_test_tensor = torch.from_numpy(X_test).float()
y_test_tensor = torch.from_numpy(y_test).float()
# 調整輸入形狀為 (seq_length, batch_size, feature_size)
X_train_tensor = X_train_tensor.unsqueeze(-1).permute(1, 0, 2)
X_test_tensor = X_test_tensor.unsqueeze(-1).permute(1, 0, 2)
注意:在 Transformer 中,常用的輸入形狀為
(seq_length, batch_size, feature_size)。如果您的版本需要不同的形狀,請根據需要調整。
import torch.nn as nn
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f'使用設備:{device}')
由於 Transformer 模型沒有內建的順序信息,我們需要添加位置編碼。
Transformer 缺乏順序信息:與 RNN 不同,Transformer 沒有內建的時間順序處理能力,無法自動感知序列中元素的位置。
引入位置信息:為了讓 Transformer 能夠理解序列中元素的順序,我們需要在輸入中加入位置信息,這就是位置編碼的作用。
數學公式:
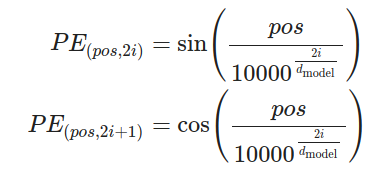
0 開始)i 個特徵維度)特性:
唯一性:每個位置 pos 都會生成一個唯一的編碼向量。
相對位置關係:位置編碼之間的關係可以表示元素之間的相對位置,因為正弦和餘弦函數具有週期性和遞增性。
直觀理解:
低頻對應長期依賴:較大的位置索引通過分母的指數增大,生成的頻率較低,對應於較長的依賴關係。
高頻對應短期依賴:較小的位置索引生成的頻率較高,對應於較短的依賴關係。
輸入:
x:形狀為 (seq\_length, batch\_size, d_{model}),包含了序列中每個元素的特徵表示。輸出:
x':與輸入張量形狀相同,將位置編碼 PE 加入到輸入張量中,即 x' = x + PE。計算位置編碼矩陣 PE:
對於每個位置 pos 和每個維度 i,計算 PE_{(pos, i)}。
使用正弦函數對偶數維度進行編碼,使用餘弦函數對奇數維度進行編碼。
將位置編碼加入輸入張量:
將位置編碼矩陣 PE 與輸入張量 x 相加。
這樣,輸入張量中的每個元素都包含了位置信息和原始特徵信息。
提供位置信息:位置編碼使得 Transformer 能夠識別序列中元素的位置,從而利用順序信息進行預測。
不改變輸入形狀:位置編碼後的張量形狀與原始輸入張量相同,方便後續在 Transformer 模型中進行計算。
輔助學習長短期依賴:透過位置編碼,模型可以更好地學習序列中元素之間的長期和短期依賴關係。
import math
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEncoding, self).__init__()
# 建立一個位置編碼矩陣
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1).float()
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term) # 偶數位置
pe[:, 1::2] = torch.cos(position * div_term) # 奇數位置
pe = pe.unsqueeze(1)
self.register_buffer('pe', pe)
def forward(self, x):
# x 的形狀為 (seq_length, batch_size, d_model)
x = x + self.pe[:x.size(0)]
return x
我們這邊就直接呼叫 Pytorch 裡的 TransformerEncoderLayer 等 Layer 加上剛剛介紹的 Positional encoding來組出 Transformer,另外更多 Transformer Detail可見連結。
class TransformerTimeSeries(nn.Module):
def __init__(self, feature_size=1, num_layers=2, nhead=4, hidden_dim=128, dropout=0.1):
super(TransformerTimeSeries, self).__init__()
self.model_type = 'Transformer'
self.input_linear = nn.Linear(feature_size, hidden_dim) # 新增的線性層
self.pos_encoder = PositionalEncoding(d_model=hidden_dim)
encoder_layers = nn.TransformerEncoderLayer(d_model=hidden_dim, nhead=nhead, dim_feedforward=hidden_dim, dropout=dropout)
self.transformer_encoder = nn.TransformerEncoder(encoder_layers, num_layers=num_layers)
self.decoder = nn.Linear(hidden_dim, 1)
self.hidden_dim = hidden_dim
def forward(self, src):
# src 形狀: (seq_length, batch_size, feature_size)
src = self.input_linear(src) # 將輸入映射到 hidden_dim 維度
src = self.pos_encoder(src)
output = self.transformer_encoder(src)
# 取最後一個時間步的輸出
output = self.decoder(output[-1, :, :])
return output
feature_size = 1 # 輸入特徵數
num_layers = 2
nhead = 4
hidden_dim = 128
model = TransformerTimeSeries(feature_size=feature_size, num_layers=num_layers, nhead=nhead, hidden_dim=hidden_dim).to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
X_train_tensor = X_train_tensor.to(device)
y_train_tensor = y_train_tensor.to(device)
X_test_tensor = X_test_tensor.to(device)
y_test_tensor = y_test_tensor.to(device)
num_epochs = 100
batch_size = X_train_tensor.size(1)
for epoch in range(num_epochs):
model.train()
optimizer.zero_grad()
output = model(X_train_tensor)
loss = criterion(output.squeeze(), y_train_tensor)
loss.backward()
optimizer.step()
if (epoch + 1) % 5 == 0:
model.eval()
with torch.no_grad():
test_output = model(X_test_tensor)
test_loss = criterion(test_output.squeeze(), y_test_tensor)
print(f'Epoch [{epoch + 1}/{num_epochs}], 訓練集 Loss: {loss.item():.4f}, 測試集 Loss: {test_loss.item():.4f}')
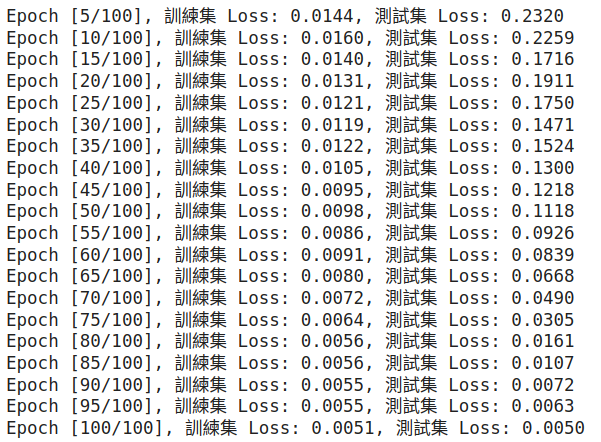
model.eval()
with torch.no_grad():
train_predict = model(X_train_tensor).cpu().numpy()
test_predict = model(X_test_tensor).cpu().numpy()
# 反歸一化
train_predict = scaler.inverse_transform(train_predict)
y_train_actual = scaler.inverse_transform(y_train_tensor.cpu().numpy().reshape(-1, 1))
test_predict = scaler.inverse_transform(test_predict)
y_test_actual = scaler.inverse_transform(y_test_tensor.cpu().numpy().reshape(-1, 1))
# 構建完整的時間序列
predicted = np.concatenate((train_predict, test_predict), axis=0)
actual = scaler.inverse_transform(dataset[lookback:])
plt.figure(figsize=(12,6))
plt.plot(actual, label='實際價格')
plt.plot(predicted, label='預測價格')
plt.title('AAPL 股票價格預測 - Transformer 模型')
plt.xlabel('時間')
plt.ylabel('價格')
plt.legend()
plt.show()
可以看到下圖: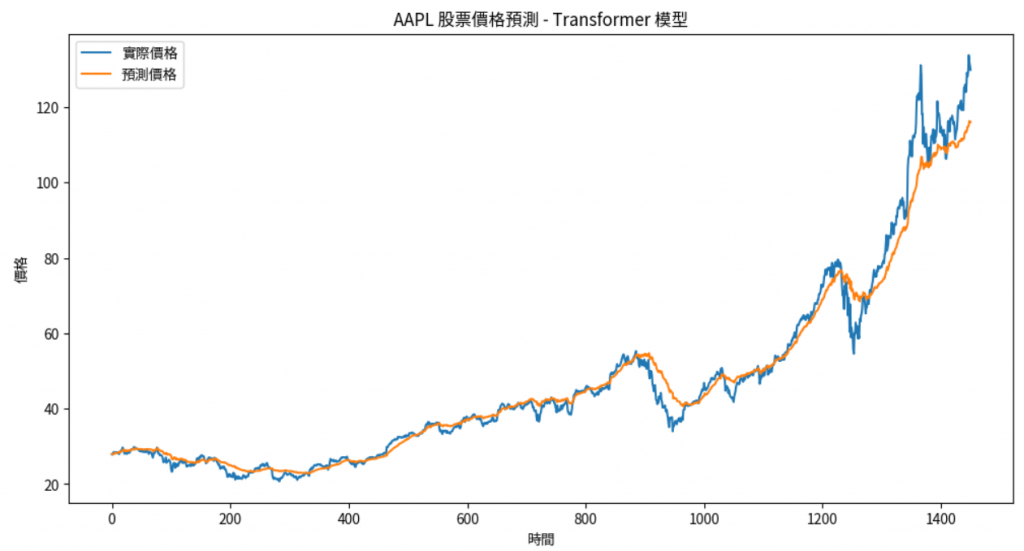
from sklearn.metrics import mean_squared_error
train_score = mean_squared_error(y_train_actual, train_predict)
test_score = mean_squared_error(y_test_actual, test_predict)
print(f'訓練集 MSE: {train_score:.2f}')
print(f'測試集 MSE: {test_score:.2f}')

lookback 天的數據來預測下一天的價格。(seq_length, batch_size, feature_size)。2、4、8。dropout,防止過擬合。多變量輸入:除了收盤價,還可以加入開盤價、最高價、最低價、成交量等特徵。
# 例如,使用多個特徵
data = data[['Close', 'Volume']]
# 需要對每個特徵進行歸一化
技術指標:添加移動平均線、相對強弱指數(RSI)等技術指標。
AdamW、SGD 等不同的優化器。MAE。為了公平地比較 Transformer 和 LSTM 模型的性能,我們將:
lookback 窗口大小(例如 60 天)。LSTM 模型:
Transformer 模型:
模型性能指標:
| 模型 | 訓練集 Loss | 測試集 Loss | 訓練集 MSE | 測試集 MSE |
|---|---|---|---|---|
| LSTM | 0.0001 | 0.0046 | 1.66 | 59.44 |
| Transformer | 0.0051 | 0.0050 | 4.12 | 63.60 |
(上述數據僅為示例,實際結果可能有所不同)
預測曲線比較:
Transformer 模型:
LSTM 模型:
優勢:
劣勢:
最終,模型的選擇應該根據具體的應用場景、數據特性和資源條件來決定。建議在實際應用中,同時嘗試多種模型,綜合考慮性能和效率,選擇最適合的解決方案。
在本節中,我們:
通過這次實踐,應該對如何使用 Transformer 模型處理時間序列數據有了更深入的理解,並掌握了使用 PyTorch 進行模型構建和訓練的基本方法。
作業:
嘗試調整 Transformer 模型的超參數:如 num_layers、nhead、hidden_dim,觀察對模型性能的影響。
增加更多的特徵:如技術指標、基本面數據,構建多變量時間序列模型。
比較 Transformer 與 LSTM 模型的性能:使用相同的數據和評價指標,分析兩者的優劣。
嘗試使用預訓練模型:如 Transformer 的變體,探索其在時間序列預測中的應用。
透過這些練習,您將能夠更靈活地應用深度學習模型進行時間序列預測,並提高模型的性能。
提示:
檢查數據形狀:在使用 Transformer 時,數據的形狀與 LSTM 不同,務必確認維度是否正確。
計算資源:Transformer 模型可能需要更多的計算資源,確保您的環境能夠支持。
防止過擬合:可以引入驗證集,使用早停(Early Stopping)等方法提高模型的泛化能力。
注意:
數據預處理的重要性:特別是在多變量輸入時,確保每個特徵都經過適當的處理。
模型的可解釋性:Transformer 模型的結構較為複雜,在金融領域的應用需要謹慎。
風險提示:股票價格預測具有高度不確定性,模型預測結果僅供參考,不應作為投資決策的唯一依據。
1.https://blogs.nvidia.com.tw/blog/what-is-a-transformer-model/
2.https://www.run.ai/guides/generative-ai/transformer-model
