矩陣（Matrix） 與基本的陣列結構息息相關，有點類似於二維陣列，它是一個利用mxn的陣列來介紹矩陣擁有m列和n行。而一般資料結構與演算法上常用到的矩陣有四種：矩陣轉置、矩陣相加、矩陣相乘、稀疏矩陣。

範例說明

1. 矩陣轉置

   • 定義：設有一mxn矩陣A，可將其轉置為nxm的矩陣B，此時AB兩矩陣為行列互換關係（即A矩陣第 i 列第 j 行元素等於B矩陣第 j 列第 i 行元素）。

     

   • 演算法：

     

   • 舉例：

     

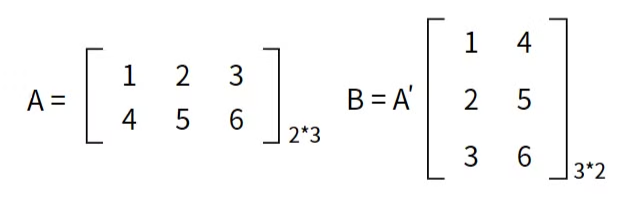
2. 矩陣相加

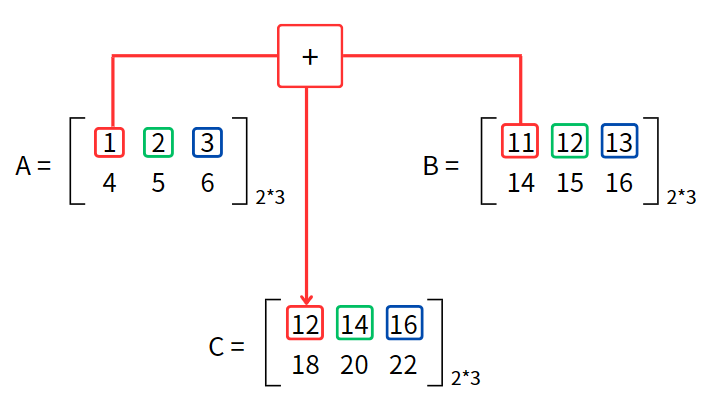
   • 定義：A,B都是mxn矩陣，將A矩陣 加上 B矩陣可以獲得一個新的C矩陣，並且此C矩陣亦為mxn矩陣。而C矩陣上第 i 列第 j 行的元素必會等於A矩陣第 i 列第 j 行的元素 加上 B矩陣第 i 列第 j 行的元素。

     

   • 演算法：

     

   • 舉例：

     

3. 矩陣相乘

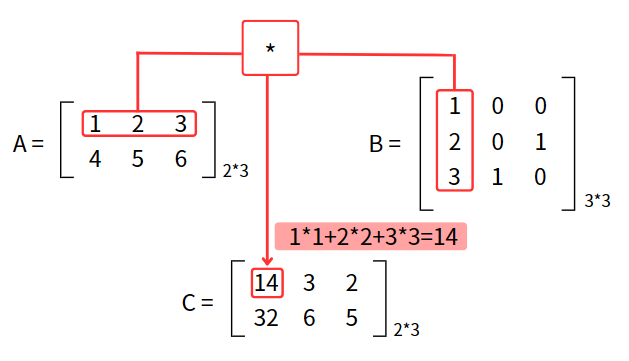
   • 定義：A為mxn矩陣、B為nxp矩陣，將A矩陣 乘上 B矩陣可以獲得一個新的C矩陣，而此C矩陣為mxp矩陣。C矩陣上第 i 列第 j 行的元素必會等於A矩陣的第 i 列 乘上 B矩陣的第 j 行（兩向量內積）。

     

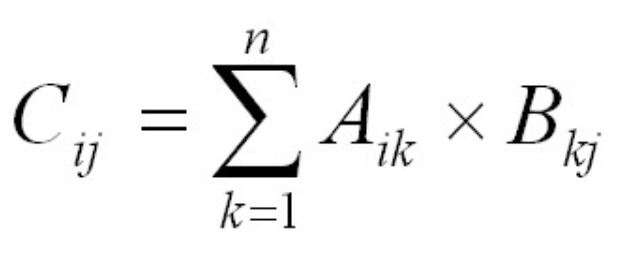
   • 演算法：

     

   • 舉例：

     

4. 稀疏矩陣

   • 定義：矩陣中大部分元素都沒有使用，元素稀稀落落，故稱稀疏矩陣。
   • 適用時機：在mxn矩陣中，多數的資料值為0。
   • 處理方法：
     • 【方法一】直接利用mxn的二為陣列來一一對應儲存。
       • 缺點：浪費時間（處理一些不必要的計算）與空間（多數為0）。
     • 【方法二】利用3-tuple結構儲存非零元素。

       • 作法：假設有一個mxn的稀疏矩陣，且其中共有k個非零元素，故準備一個二為矩陣A[0…k,0…2]。

         

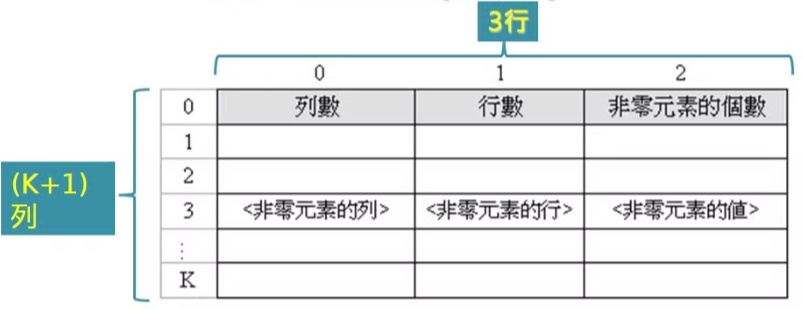
       • 優點：只儲存非零資料，減少記憶體空間的浪費。

5. 還有這些特殊矩陣…，例如：上三角矩陣與下三角矩陣。

矩陣是一種常見的資料結構，它的優缺點取決於使用的場景：

優點：

• 直觀易理解：矩陣很適合用來表示表格數據，例如圖像、地圖或棋盤，這些資料具有明確的行與列的結構。
• 快速存取：矩陣的元素可以透過索引直接存取，時間複雜度為 O(1)，特別適合處理需要頻繁隨機存取的資料。
• 適合數學運算：矩陣廣泛應用於數學計算、線性代數和圖形學中，能有效地進行矩陣加法、乘法等運算。

缺點：

• 固定大小：矩陣的大小在初始化時就必須決定，擴展或縮小矩陣非常困難且耗時，不適合處理動態大小的資料。
• 空間效率低：如果矩陣中有很多未使用的空間（稀疏矩陣），會浪費大量記憶體資源。對於這種情況，可能需要採用其他資料結構，如鏈結串列或壓縮存儲形式。
• 插入與刪除成本高：如果要在矩陣中插入或刪除元素，可能需要移動大量元素，這樣的操作在大矩陣上效能會變差。

參考資料：

1. 吳燦銘、胡昭民(2018)。《圖解資料結構-使用Java(第三版)》。新北：博碩文化。
2. 吳燦銘、胡昭民(2020)。《圖說演算法：使用Java》。新北：博碩文化。
3. 李春雄(2021)。《動畫圖解APP資料結構─使用Java》。台中：滄海出版。
4. 胡昭民 (2023)。《圖解資料結構 × 演算法：運用 Python 結合 ChatGPT 輔助驗證及寫程式》。新北：博碩文化。