Collision

When two or more objects happen to be hashed into the same index in the hash table.

當兩個以上的 element 經過 hash function 卻產生了相同的 hash value(key/index of hash table)，導致多個元素會存在同一個位置的衝突狀態，就稱為 hash collision

Load factor of a Hash Table

The load factor is a measure that typically ranges between 0 and 1 and is defined as n/m, where:

n = the numbers of elements to store in the hash table.
m = the size of a hash table

So, 0 < n/m < 1 or 0 < n < m

A higher m(size of the hash table) usually results in fewer chances of collision because there are more available slots to distribute the elements. Ideally, the size of the hash table should be larger than the numbers of elements(m>n) to minimize collisions.

However, a larger hash table takes up more memory and results in wasted space, as many of the slots could remain empty. Therefore, it's not practical to make an extremly large hash table to avoid collisions.

--

當 load factor 越大，發生 collision 的情況也會隨著增加，基本上 hashtable 的大小必定要大於等於欲存取於 hashtable 內元素的數量，以盡可能避免 collision 的發生

然而，hashtable 越大，所佔據的記憶體也越多，且其中的空位也會跟著變多造成記憶體的浪費，所以實際上也不會一味增加 hashtable 的大小來避免 collision 的發生

Handling with Collision

• No matter what hash function we use, we'll have collisions.
• A collision can be handled using various technique, such as Separate Chaining & Open Addressing

--

• 不管用哪種hash function，仍無法避免可能出現 collisions
• 當遇到 collisions 時，可以用 鏈結(Separate Chaining) & 開放定址(Open Addressing) 來處理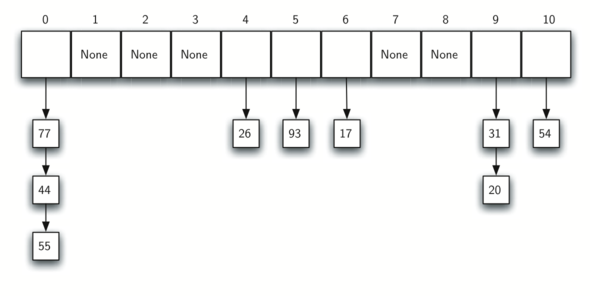

Separate Chaining Technique

In separate chaining, each slot of the hash table holds a collection (like an array or linked list) of all elements that hash to the same index.

So, Chaining allows many items to excist at the same location in the hash table.

--

將每個 hash table 的每個 slot 設計成 linked list 或 array，
當兩元素產生相同 hash value 的 collision時 ，新的元素串接在既有元素的後面，這個技巧就稱為鏈接

所以，鏈接允許多個元素共同存在於同一個 hash table 的位置

Load factor of Separate chaining

Advantage of Separate Chaining

• Simple to implement
• Each slot can hold multiple elements, reducing the impact of a high load factor.
• Ideal for situations where the number of items or the frequency of key insertions/delection is unpredictable.

--

• 邏輯簡單容易達成
• 每個 slot 可儲存多個元素，即便 load factor 很大也不受到影響
• 適用於當不確定有多少元素要被加入或移除的時候

Disadvantage of Separate Chaining

• Require extra space to store additional elements.
• The time complexity of searching a specific element can degrade to O(n) as the chains grow longer.
• Poor cache performance, as the elements are stored in linked list or arrays.
• Might wasted space in the hash table due to empty slots.

--

• 需要更多空間去儲存額外的元素
• 如果單一個 slot 中儲存很多個元素，那在單一 slot 中尋找特定元素的時間複雜度將會來到O(n)
• 當元素儲存於linked list或array中，快取效能並不好
• 因為 hash table 內可能會有空的 slot，導致空間上的浪費

Open Addressing Technique

In open addressing, if a hashed key's initial position in a hash table is already occupied, a probing sequence is used to locate the next available slot. This sequence checks alternate indices based on a specific offset pattern until an empty slot is found for the key.

Since the open addressing not allow multiple elements to reside in the same slot, the load factor of the hash table becomes important.(load factor need to be < 1)

There're some common probing sequence:

• Linear Probing
• Quadratic probing
• Double hashing

--

如果某個 hashed key 的位置已有其他元素，則使用探測(probing)來找仍未儲存資料的儲存空間，簡單來講就是『找下一個index』的 slot 是否被佔用

目標 index 滿了就換位子，而找哪個位子的方法則為探測(probing sequence)

因為開放尋址不允許多個元素儲存於 hash table 上相同 index，所以 hash table 的 load factor 便相當重要（load factor 不可超過 1）

常見的探測方法有：

• 線性探測(Linear Probing)
• 平方探測(Quadratic Probing)
• 雙重雜湊(Double Hashing)

Load factor of Open Addressing

The performance of open addressing becomes very bad when the load factor approache 1. So if the load factor is approaching the threshold, we need to grow the hash table size (ideally exponentially, e.g. double).

--

因為開放定址的原理是『找雜湊表的空位去儲存碰撞的元素』，所以 load factor 必不能超過 1（表示雜湊表已沒有空位），且當 load factor 的值趨近於 1 的時候，其效能極差（越難找到空位），所以當 load factor 趨近臨界值的時候，我們需要增加雜湊表的長度（理想情況下呈指數增長，如雙倍）

Probing function

There are countless amount of probing sequence you can come up with, there're a few:

k = key value

• Linear probing
  P(x) = ax+b, where a, b are constants.
• Quadratic probing
  P(x) = ax^2+bx+c, where a, b, c are constants.
• Double hashing
  P(k,x) = x * H2(k) , where H2(k) is a secondary hash function.
• Psesudo random number generator
  P(k,x) = x * RNG(H(k) , x), where RNG is a random number generator seeded with H(k).

Linear probing

• Beware of infinite loop!
  if our linear function is: Lp(x) = 3x
  hash function is:H(k) = 4
  and the length of hash table is 9 (N=9), we end up with cycle occurring:

H(k)+P(0) mod N = 4+0 % 9 = 4
H(k)+P(1) mod N = 4+3 % 9 = 7
H(k)+P(2) mod N = 4+6 % 9 = 1
H(k)+P(3) mod N = 4+9 % 9 = 4
H(k)+P(4) mod N = 4+12 % 9 = 7
H(k)+P(5) mod N = 4+15 % 9 = 1
...
The cycle {4,7,1} makes it impossiable to reach {0,2,3,5,6,8}
so if {4,7,1} is occupied, it will cause a infinite loop!

Lp(x) = ax , N length of hashtable
If we want to loop through the empty bucket in hash table, the Greatest Common Denominator of (a,N) must to be 1.

Advantage of Open Addressing

• Better cache performance, as all elements are stored in a single table.
• Requires less memory for smaller record sizes.

Disadvantage of Open Addressing

• As the load factor approaches 1, the efficiency of Open Addressing decreases significantly.
• Requires additional computation to handle clustering, which can slow down performance.

Implement separate chaining & open addressing with javascript

附上 codepen 如下：

Separate chaining

Open addressing with linear probing 的版本，如果有興趣的話也可以試試寫出其他的 probing method

其他資源

Hash table
https://en.wikipedia.org/wiki/Hash_table
Hash collision
https://en.wikipedia.org/wiki/Hash_collision
Hash Tables, Hashing and Collision Handling
https://medium.com/codex/hash-tables-hashing-and-collision-handling-8e4629506572
Separate Chaining Collision Handling Technique In Hashing
https://www.geeksforgeeks.org/separate-chaining-collision-handling-technique-in-hashing/

Linear Probing
https://youtu.be/Ma9XOInZJWM?si=ujAJaZYipmq7tqT9&t=191